class: center, middle, inverse, title-slide .title[ # Computational Statistics ] .subtitle[ ## Lecture 9 ] .author[ ### Yixuan Qiu ] .date[ ### 2023-11-08 ] --- class: inverse, center, middle # Optimization --- # Last Time - We have spent much time on nonsmooth problems - Since they are very common in statistical models - Meanwhile they are considered "hard problems" in convex optimization - So far, the main tool to overcome nonsmoothness is the proximal operator - Seen in proximal gradient descent, Douglas-Rachford splitting, Davis-Yin splitting, etc. - In this lecture we introduce a few other frameworks --- # Today's Topics - Alternating direction method of multipliers - Coordinate descent - Case studies --- class: inverse, center, middle # Alternating Direction Method of Multipliers --- # Problem Another popular framework to deal with nonsmooth or constrained problems is the alternating direction method of multipliers (ADMM). It considers problems of the form: `$$\begin{align*} \min_{x,z} & \quad F(x,z):=f(x)+g(z)\\ \text{subject to} & \quad Ax+Bz=c \end{align*}$$` - `\(x\in\mathbb{R}^n\)`, `\(z\in\mathbb{R}^m\)`, `\(A\in\mathbb{R}^{p\times n}\)`, `\(B\in\mathbb{R}^{p\times m}\)`, and `\(c\in\mathbb{R}^p\)`. - `\(f(x)\)` and `\(g(z)\)` are convex functions, possibly nonsmooth - `\(Ax+Bz=c\)` represents general linear equality constraints --- # Examples - Although this problem form is a bit exotic compared with those we have seen in previous lectures - Many familiar problems can be converted into this form by cleverly defining the `\(x\)` and `\(z\)` variables - Lasso: `$$\min_x\ \frac{1}{2}\Vert b-Ax\Vert^{2}+\lambda\Vert x\Vert_{1}$$` - `\(f(x)=(1/2)\Vert b-Ax\Vert^{2}\)`, `\(g(z)=\lambda\Vert z\Vert_1\)` - Linear constraint `\(x-z=0\)` --- # Examples - Least absolute deviations: `$$\min_x\ \Vert b-Ax \Vert_1$$` - `\(f(x)=0\)`, `\(g(z)=\Vert z\Vert_1\)` - Linear constraint `\(Ax-z=b\)` --- # Algorithm ADMM can be expressed as the following algorithm. Given initial values `\(z^{(0)}\)` and `\(u^{(0)}\)`, for `\(k=0,1\ldots\)`, iterate `$$\begin{align*} x^{(k+1)} & =\underset{x}{\arg\min}\ f(x)+(\rho/2)\Vert Ax+Bz^{(k)}-c+u^{(k)}\Vert^{2}\\ z^{(k+1)} & =\underset{z}{\arg\min}\ g(z)+(\rho/2)\Vert Ax^{(k+1)}+Bz-c+u^{(k)}\Vert^{2}\\ u^{(k+1)} & =u^{(k)}+Ax^{(k+1)}+Bz^{(k+1)}-c \end{align*}$$` `\(\rho>0\)` is an arbitray "inverse step size" parameter. --- # Some Remarks - The `\(x\)`- and `\(z\)`-updates look similar to proximal operators - However, here we have more general quadratic terms - This means that the `\(x\)`- and `\(z\)`-updates are typically more difficult than proximal operators - On the other hand, ADMM does not need to explicitly project to the linear constraint set - These findings largely guide how to define the `\(f\)` and `\(g\)` functions --- # Relation with DRS Consider using ADMM to solve the problem `$$\min_{x}\ f(x)+g(x)\Leftrightarrow\min_{x,z}\ f(x)+g(z)\ \text{ subject to }\ x-z=0$$` Then the iteration becomes `$$\begin{align*} x^{(k+1)} & =\mathbf{prox}_{(1/\rho)f}(z^{(k)}-u^{(k)})\\ z^{(k+1)} & =\mathbf{prox}_{(1/\rho)g}(x^{(k+1)}+u^{(k)})\\ u^{(k+1)} & =u^{(k)}+x^{(k+1)}-z^{(k+1)} \end{align*}$$` This is equivalent to DRS, by slightly reparameterizing the variables. --- # Implementation Details - Many implementation details can be found in the main reference [[1]](https://web.stanford.edu/~boyd/papers/pdf/admm_distr_stats.pdf) - Stopping criterion - Selection of the `\(\rho\)` parameter - Closed-form expressions for specific problems --- # Convergence Property ^{<span class="small">[2]</span>} The sequence `\((x^{(k)},z^{(k)},u^{(k)})\)` satisfy `$$\small\Vert A(x^{(k+1)}-x^{(k)})\Vert^2+\Vert B(z^{(k+1)}-z^{(k)})\Vert^2+\Vert u^{(k+1)}-u^{(k)}\Vert^2=o(1/k).$$` This is one of the most general convergence results on ADMM. Many other faster rates exist by imposing stronger conditions on `\(f(x)\)` and `\(g(z)\)`, e.g. smoothness, strong convexity, etc. --- class: center, middle # Coordinate Descent --- # Motivation - One more idea to overcome nonsmoothness is to directly find the optimal point of nonsmooth problems - Of course, this is unrealistic for general problems - But in many cases this is possible for univariate functions --- # Example Lasso model `$$\min_\beta\ \ell(\beta):=\min_\beta\ \frac{1}{2n}\Vert y-X\beta\Vert^{2}+\lambda\Vert \beta\Vert_{1}$$` - Solving the whole `\(\beta\)` vector is hard - However, assume we fix all elements of `\(\beta\)` except `\(\beta_i\)` - Then we can actually derive the optimal `\(\beta_i\)` in closed form --- # Example - Recall that in Lecture 7 we have shown `$$f(x^*)=\min_{x}\,f(x)\Leftrightarrow 0\in \partial f(x^*)$$` - View `\(\tilde{\ell}(\beta_i)\equiv\ell(\beta)\)` as a function of `\(\beta_i\)`, then `$$\partial\tilde{\ell}(\beta_{i})=n^{-1}\Vert X_{i}\Vert^2\beta_{i}+n^{-1}X_{i}'(X_{-i}\beta_{-i}-y)+\lambda\partial|\beta_{i}|,$$` - `\(X_i\)` is the `\(i\)`-column of `\(X\)` - `\(X_{-i}\)` is the matrix formed by removing `\(X_i\)` from `\(X\)` - `\(\beta_{-i}\)` is the vector formed by removing `\(\beta_i\)` from `\(\beta\)` --- # Example - `\(0\in \partial\tilde{\ell}(\beta_{i})\)` gives the solution `$$\beta_{i}=\mathcal{S}_{n\lambda/\Vert X_{i}\Vert^{2}}\left(\frac{X_{i}'(y-X_{-i}\beta_{-i})}{\Vert X_{i}\Vert^{2}}\right)$$` --- # Coordinate Descent These findings motivate the coordinate descent (CD) algorithm. Consider the problem `$$\min_x\ f(x):=\min_x\ f(x_1,\ldots,x_n)$$` One common type of CD algorithm proceeds as follows. Given initial value `\(x^{(0)}\)`, for `\(k=0,1,\ldots\)`, iterate: `$$x_{i}^{(k+1)}=\underset{x_{i}}{\arg\min}\ f(x_{1}^{(k+1)},\ldots,x_{i-1}^{(k+1)},x_{i},x_{i+1}^{(k)},\ldots,x_{n}^{(k)})$$` for `\(i=1,\ldots,n\)` within each `\(k\)`-outer-iteration. This is typically called the .highlight[cyclic CD] algorithm. --- # Variants Another popular variant is to randomly select a coordinate to update. Given initial value `\(x^{(0)}\)`, for `\(k=0,1,\ldots\)`, do: 1. Randomly select `\(i_k\)` from `\(\{1,2,\ldots,n\}\)` with equal probabilities 2. Fixing other coordinates and update `$$\begin{align*} x_{i_{k}}^{(k+1)} & =\underset{x_{i_{k}}}{\arg\min}\ f(x_{1}^{(k)},\ldots,x_{i_{k}-1}^{(k)},x_{i_{k}},x_{i_{k}+1}^{(k)},\ldots,x_{n}^{(k)})\\ x_{j}^{(k+1)} & =x_{j}^{(k)},\quad j\neq i_{k} \end{align*}$$` In the literature, this method is sometimes called .highlight[randomized CD]. --- # Variants Many other variants exist: - .highlight[Permutation CD]: for each `\(k\)`, use a random permutation of `\(\{1,2,\ldots,n\}\)` to define the order of coordinate updates - .highlight[Block CD]: each time update a block of coordinates simultaneously, instead of a single coordinate - .highlight[Coordinate proximal gradient descent]: use proximal operators to update coordinates - ... --- # Convergence Property ^{<span class="small">[3]</span>} Unfortunately, CD does not always converge to an optimal point for nonsmooth `\(f\)`. Instead, consider the problem `$$f(x)=g(x)+\sum_{i=1}^n h_i(x_i),$$` where `\(g(x)\)` is convex and differentiable, and each `\(h_i(x_i)\)` is convex, possibly nonsmooth. [3] shows that with very mild regularity conditions, the CD iterates `\(x^{(k)}\)` converge to an optimal point of `\(f(x)\)`. The result holds for .highlight[block CD] and .highlight[arbitrary order] of cycle through coordinates. --- # Convergence Property ^{<span class="small">[4]</span>} There exist many convergence results for different variants of CD based on different assumptions on `\(f(x)\)`. Below is one representative result with weak assumptions. Assume that `\(g(x)\)` is coordinate-wise `\(L_i\)`-smooth, and define `$$\small R_{0}=\max_{y}\max_{x^{\\*}\in\mathcal{X}^{\\*}}\left\{ \left(\sum_{i=1}^{n}L_{i}(y_{i}-x_{i}^{\\*})^{2}\right)^{1/2}:f(y)\le f(x^{(0)})\right\},$$` where `\(\mathcal{X}^*\)` denotes the optimal set. (See next slide) --- # Convergence Property ^{<span class="small">[4]</span>} Consider the randomized CD algorithm. Fix a confidence parameter `\(0<\rho<1\)` and an accuracy level `\(\varepsilon < \min\{R_0^2,f(x^{(0)})-f(x^*)\}\)`. Then with `$$k\ge \frac{2nR_{0}^{2}}{\varepsilon}\log\frac{f(x^{(0)})-f(x^{*})}{\varepsilon\rho},$$` we have `\(f(x^{(k)})-f(x^*)\le \varepsilon\)` with probability at least `\(1-\rho\)`. --- ## Convergence with Strong Convexity ^{<span class="small">[4]</span>} For simplicity suppose `\(L_i\equiv L\)`, and assume that `\(g(x)\)` is also strongly convex with parameter `\(m>0\)`. Fix a confidence parameter `\(0<\rho<1\)` and an accuracy level `\(\varepsilon>0\)`. If `$$k\ge\frac{4Ln}{m}\log\frac{f(x^{(0)})-f(x^{*})}{\varepsilon\rho},$$` then `\(f(x^{(k)})-f(x^*)\le \varepsilon\)` with probability at least `\(1-\rho\)`. --- class: center, middle # Case Study --- # Lasso We use the lasso model `$$\min_\beta\ \ell(\beta):=\min_\beta\ \frac{1}{2n}\Vert y-X\beta\Vert^{2}+\lambda\Vert \beta\Vert_{1}$$` to study the convergence property and computational efficiency of several algorithms we have covered in previous lectures. - Derive the update rules for several algorithms - Study the change of loss function versus iteration number - Study the change of loss function versus running time --- # Simulate Data Set The design matrix is a simulated sparse matrix, but we tentatively use its dense version. ```r library(Matrix) set.seed(123) n = 500 p = 1000 s = 30 xsp = rsparsematrix(n, p, density = 0.1) x = as.matrix(xsp) beta = c(rnorm(s), numeric(p - s)) y = as.numeric(xsp %*% beta) + 0.1 * rnorm(n) lam = 0.001 objfn = function(beta, x, y, lam) { 0.5 * mean((y - as.numeric(x %*% beta))^2) + lam * sum(abs(beta)) } ``` --- # Compute Optimal Value Use the celebrated **glmnet** package to compute the optimal value. ```r library(glmnet) res = glmnet(x, y, lambda = lam, thresh = 1e-15, standardize = FALSE, intercept = FALSE) beta_opt = as.numeric(res$beta) head(beta_opt) ``` ``` ## [1] -0.3862279 1.4304118 -0.2206914 1.1256892 0.1704705 0.8657187 ``` ```r tail(beta_opt) ``` ``` ## [1] 0.000000000 -0.003938278 0.000000000 0.000000000 0.000000000 ## [6] 0.008219107 ``` ```r obj_opt = objfn(beta_opt, x, y, lam) obj_opt ``` ``` ## [1] 0.02782515 ``` --- # Optimization A general interface for running optimization algorithms. ```r run_opt = function(x, y, lam, init_state, update_rule, maxit = 1001, ...) { ... } ``` - `init_state()` and `update_rule()` are two function arguments to characterize the optimization algorithm - `init_state(x, y, lam, ...)` is used to create initial state of the algorithm - `update_rule(beta, iter, x, y, lam, state)` returns the updated `\(\beta\)` and state, `list(beta, state)` --- # Optimization A general interface for running optimization algorithms. ```r run_opt = function(x, y, lam, init_state, update_rule, maxit = 1001, ...) { p = ncol(x) beta_hat = numeric(p) losses = c() # Initialization state = init_state(x, y, lam, ...) # Main loop for(i in 1:maxit) { res = update_rule(beta_hat, i - 1, x, y, lam, state) beta_hat = res$beta state = res$state loss = objfn(beta_hat, x, y, lam) losses = c(losses, loss) if((i - 1) %% 100 == 0) cat(sprintf("Iter %d, loss = %.6f\n", i - 1, loss)) } list(beta_hat = beta_hat, losses = losses) } ``` --- # Subgradient Method - Choose `\(\tilde{\nabla}\ell(\beta)=(1/n)X'(X\beta-y)+\lambda\cdot\mathrm{sign}(\beta)\)` - Update rule: `$$\beta^{(k+1)}=\beta^{(k)}-\alpha_{k}\tilde{\nabla}\ell(\beta^{(k)})$$` - Step size `\(\alpha_k=\alpha_0/\sqrt{k+1}\)` --- # Implementation ```r init_subgrad = function(x, y, lam, alpha0 = 1) { list(alpha0 = alpha0) } update_subgrad = function(beta, k, x, y, lam, state) { n = nrow(x) alpha0 = state$alpha0 alphak = alpha0 / sqrt(k + 1) Xtr = crossprod(x, as.numeric(x %*% beta) - y) subgrad = as.numeric(Xtr) / n + lam * sign(beta) new_beta = beta - alphak * subgrad list(beta = new_beta, state = state) } ``` --- # Result ```r res_subgrad1 = run_opt( x, y, lam, init_subgrad, update_subgrad, alpha0 = 1) ``` ``` ## Iter 0, loss = 0.770908 ## Iter 100, loss = 0.084973 ## Iter 200, loss = 0.074552 ## Iter 300, loss = 0.070417 ## Iter 400, loss = 0.067906 ## Iter 500, loss = 0.066074 ## Iter 600, loss = 0.064626 ## Iter 700, loss = 0.063428 ## Iter 800, loss = 0.062394 ## Iter 900, loss = 0.061477 ## Iter 1000, loss = 0.060661 ``` ```r head(res_subgrad1$beta) ``` ``` ## [1] -2.174641e-01 9.316010e-01 -1.026982e-01 6.878443e-01 1.129936e-05 ## [6] 2.784390e-01 ``` ```r tail(res_subgrad1$beta) ``` ``` ## [1] -3.352589e-02 -5.879592e-02 -1.432275e-06 -3.051985e-02 5.442229e-02 ## [6] 1.141592e-01 ``` --- # Result ```r res_subgrad10 = run_opt( x, y, lam, init_subgrad, update_subgrad, alpha0 = 10) ``` ``` ## Iter 0, loss = 8.881744 ## Iter 100, loss = 0.049232 ## Iter 200, loss = 0.040807 ## Iter 300, loss = 0.036166 ## Iter 400, loss = 0.032993 ## Iter 500, loss = 0.030828 ## Iter 600, loss = 0.029429 ## Iter 700, loss = 0.028636 ## Iter 800, loss = 0.028227 ## Iter 900, loss = 0.028043 ## Iter 1000, loss = 0.027961 ``` ```r head(res_subgrad10$beta) ``` ``` ## [1] -0.3913635 1.4284850 -0.2179803 1.1101840 0.1683580 0.8471952 ``` ```r tail(res_subgrad10$beta) ``` ``` ## [1] -2.979032e-04 -3.842055e-03 2.795830e-04 -9.758347e-05 -1.092878e-04 ## [6] 1.166201e-02 ``` --- # Proximal Gradient Descent - Update rule: `$$\beta^{(k+1)}=\mathcal{S}_{\alpha\lambda}\left(\beta^{(k)}-(\alpha/n)X'(X\beta^{(k)}-y)\right)$$` - Step size `\(\alpha=1/\lambda_\max(n^{-1}X'X)=n/\lambda_\max(X'X)\)` --- # Implementation ```r library(RSpectra) # Soft-thresholding function soft_thresh = function(x, a) { sign(x) * pmax(0, abs(x) - a) } init_ista = function(x, y, lam) { # Compute the largest eigenvalue of X'X alpha = nrow(x) / svds(x, k = 1, nu = 0, nv = 0)$d^2 list(alpha = alpha) } update_ista = function(beta, k, x, y, lam, state) { n = nrow(x) alpha = state$alpha Xtr = crossprod(x, as.numeric(x %*% beta) - y) grad = as.numeric(Xtr) / n new_beta = soft_thresh(beta - alpha * grad, alpha * lam) list(beta = new_beta, state = state) } ``` --- # Result ```r res_ista = run_opt(x, y, lam, init_ista, update_ista) ``` ``` ## Iter 0, loss = 0.494847 ## Iter 100, loss = 0.044493 ## Iter 200, loss = 0.032321 ## Iter 300, loss = 0.028040 ## Iter 400, loss = 0.027830 ## Iter 500, loss = 0.027825 ## Iter 600, loss = 0.027825 ## Iter 700, loss = 0.027825 ## Iter 800, loss = 0.027825 ## Iter 900, loss = 0.027825 ## Iter 1000, loss = 0.027825 ``` ```r head(res_ista$beta) ``` ``` ## [1] -0.3862280 1.4304114 -0.2206905 1.1256887 0.1704708 0.8657158 ``` ```r tail(res_ista$beta) ``` ``` ## [1] 0.000000000 -0.003938134 0.000000000 0.000000000 0.000000000 ## [6] 0.008219716 ``` --- # Accelerated Proximal Gradient Descent - Update rule: `$$\begin{align*} u^{(k+1)} & =\beta^{(k)}+\frac{k-1}{k+2}(\beta^{(k)}-\beta^{(k-1)})\\ \beta^{(k+1)} & =\mathcal{S}_{\alpha\lambda}\left(u^{(k)}-(\alpha/n)X'(Xu^{(k)}-y)\right) \end{align*}$$` - Step size `\(\alpha=1/\lambda_\max(n^{-1}X'X)=n/\lambda_\max(X'X)\)` --- # Implementation ```r init_fista = function(x, y, lam) { p = ncol(x) alpha = nrow(x) / svds(x, k = 1, nu = 0, nv = 0)$d^2 list(alpha = alpha, old_beta = numeric(p), betau = numeric(p)) } update_fista = function(beta, k, x, y, lam, state) { n = nrow(x) alpha = state$alpha state$betau = if(k <= 1) beta else beta + (k - 1) / (k + 2) * (beta - state$old_beta) Xtr = crossprod(x, as.numeric(x %*% state$betau) - y) grad = as.numeric(Xtr) / n new_beta = soft_thresh(state$betau - alpha * grad, alpha * lam) state$old_beta = beta list(beta = new_beta, state = state) } ``` --- # Result ```r res_fista = run_opt(x, y, lam, init_fista, update_fista) ``` ``` ## Iter 0, loss = 0.494847 ## Iter 100, loss = 0.027830 ## Iter 200, loss = 0.027825 ## Iter 300, loss = 0.027825 ## Iter 400, loss = 0.027825 ## Iter 500, loss = 0.027825 ## Iter 600, loss = 0.027825 ## Iter 700, loss = 0.027825 ## Iter 800, loss = 0.027825 ## Iter 900, loss = 0.027825 ## Iter 1000, loss = 0.027825 ``` ```r head(res_fista$beta) ``` ``` ## [1] -0.3862278 1.4304116 -0.2206913 1.1256895 0.1704706 0.8657180 ``` ```r tail(res_fista$beta) ``` ``` ## [1] 0.000000000 -0.003938369 0.000000000 0.000000000 0.000000000 ## [6] 0.008219289 ``` --- # Douglas-Rachford Splitting - Let `\(g(\beta)=\lambda\Vert \beta\Vert_{1}\)`, `\(f(\beta)=\frac{1}{2n}\Vert y-X\beta\Vert^{2}\)`. Then `$$\begin{align*} \mathbf{prox}_{\alpha g}(z) & =\mathcal{S}_{\alpha\lambda}(z)\\ \mathbf{prox}_{\alpha h}(\beta) & =(I+(\alpha/n)X'X)^{-1}(\beta+(\alpha/n)X'y) \end{align*}$$` - Update rule: `$$\begin{align*} \beta^{(k+1)} & =\mathcal{S}_{\alpha\lambda}\left(u^{(k)}\right)\\ u^{(k+1)} & =u^{(k)}+A^{-1}(2\beta^{(k+1)}-u^{(k)}+(\alpha/n)X'y)-\beta^{(k+1)} \end{align*}$$` where `\(A=I+(\alpha/n)X'X\)` --- # Implementation ```r chol_solve = function(R, b) { y = backsolve(R, b, transpose = TRUE) # R'*y = b x = backsolve(R, y) # R*x = y x } init_drs = function(x, y, lam, alpha = 1) { n = nrow(x) p = ncol(x) scaled_xty = alpha / n * as.numeric(crossprod(x, y)) R = chol(diag(p) + alpha / n * crossprod(x)) list(alpha = alpha, sxty = scaled_xty, R = as.matrix(R), betau = numeric(p)) } update_drs = function(beta, k, x, y, lam, state) { n = nrow(x) alpha = state$alpha new_beta = soft_thresh(state$betau, alpha * lam) rhs = 2 * new_beta - state$betau + state$sxty state$betau = state$betau + chol_solve(state$R, rhs) - new_beta list(beta = new_beta, state = state) } ``` --- # Result ```r res_drs1 = run_opt(x, y, lam, init_drs, update_drs, alpha = 1) ``` ``` ## Iter 0, loss = 1.454710 ## Iter 100, loss = 0.053128 ## Iter 200, loss = 0.041675 ## Iter 300, loss = 0.034461 ## Iter 400, loss = 0.029864 ## Iter 500, loss = 0.028097 ## Iter 600, loss = 0.027848 ## Iter 700, loss = 0.027828 ## Iter 800, loss = 0.027826 ## Iter 900, loss = 0.027825 ## Iter 1000, loss = 0.027825 ``` ```r head(res_drs1$beta) ``` ``` ## [1] -0.3863738 1.4304559 -0.2205224 1.1254740 0.1704870 0.8652928 ``` ```r tail(res_drs1$beta) ``` ``` ## [1] 0.000000000 -0.003902763 0.000000000 0.000000000 0.000000000 ## [6] 0.008261868 ``` --- # Result ```r res_drs10 = run_opt(x, y, lam, init_drs, update_drs, alpha = 10) ``` ``` ## Iter 0, loss = 1.454710 ## Iter 100, loss = 0.027825 ## Iter 200, loss = 0.027825 ## Iter 300, loss = 0.027825 ## Iter 400, loss = 0.027825 ## Iter 500, loss = 0.027825 ## Iter 600, loss = 0.027825 ## Iter 700, loss = 0.027825 ## Iter 800, loss = 0.027825 ## Iter 900, loss = 0.027825 ## Iter 1000, loss = 0.027825 ``` ```r head(res_drs10$beta) ``` ``` ## [1] -0.3862278 1.4304117 -0.2206913 1.1256895 0.1704706 0.8657182 ``` ```r tail(res_drs10$beta) ``` ``` ## [1] 0.000000000 -0.003938377 0.000000000 0.000000000 0.000000000 ## [6] 0.008219268 ``` --- # ADMM - Let `\(f(\beta)=\lambda\Vert \beta\Vert_{1}\)`, `\(g(\beta)=\frac{1}{2n}\Vert y-X\beta\Vert^{2}\)`. Then - Update rule: `$$\begin{align*} \beta^{(k+1)} & =\mathcal{S}_{\lambda/\rho}\left(z^{(k)}-u^{(k)}\right)\\ z^{(k+1)} & =A^{-1}(\beta^{(k+1)}+u^{(k)}+(n\rho)^{-1}X'y)\\ u^{(k+1)} & =u^{(k)}+\beta^{(k+1)}-z^{(k+1)} \end{align*}$$` where `\(A=I+(n\rho)^{-1}X'X\)` - A reparameterized DRS --- # Implementation ```r init_admm = function(x, y, lam, rho = 1) { n = nrow(x) p = ncol(x) scaled_xty = as.numeric(crossprod(x, y)) / n / rho R = chol(diag(p) + crossprod(x) / n / rho) list(rho = rho, sxty = scaled_xty, R = as.matrix(R), betaz = numeric(p), betau = numeric(p)) } update_admm = function(beta, k, x, y, lam, state) { n = nrow(x) rho = state$rho new_beta = soft_thresh(state$betaz - state$betau, lam / rho) rhs = new_beta + state$betau + state$sxty state$betaz = chol_solve(state$R, rhs) state$betau = state$betau + new_beta - state$betaz list(beta = new_beta, state = state) } ``` --- # Result ```r res_admm1 = run_opt(x, y, lam, init_admm, update_admm, rho = 1) ``` ``` ## Iter 0, loss = 1.454710 ## Iter 100, loss = 0.053098 ## Iter 200, loss = 0.041664 ## Iter 300, loss = 0.034453 ## Iter 400, loss = 0.029859 ## Iter 500, loss = 0.028096 ## Iter 600, loss = 0.027848 ## Iter 700, loss = 0.027828 ## Iter 800, loss = 0.027826 ## Iter 900, loss = 0.027825 ## Iter 1000, loss = 0.027825 ``` ```r head(res_admm1$beta) ``` ``` ## [1] -0.3863737 1.4304559 -0.2205226 1.1254743 0.1704871 0.8652934 ``` ```r tail(res_admm1$beta) ``` ``` ## [1] 0.000000000 -0.003902788 0.000000000 0.000000000 0.000000000 ## [6] 0.008261821 ``` --- # Result ```r res_admm0.1 = run_opt(x, y, lam, init_admm, update_admm, rho = 0.1) ``` ``` ## Iter 0, loss = 1.454710 ## Iter 100, loss = 0.027825 ## Iter 200, loss = 0.027825 ## Iter 300, loss = 0.027825 ## Iter 400, loss = 0.027825 ## Iter 500, loss = 0.027825 ## Iter 600, loss = 0.027825 ## Iter 700, loss = 0.027825 ## Iter 800, loss = 0.027825 ## Iter 900, loss = 0.027825 ## Iter 1000, loss = 0.027825 ``` ```r head(res_admm0.1$beta) ``` ``` ## [1] -0.3862278 1.4304117 -0.2206913 1.1256895 0.1704706 0.8657182 ``` ```r tail(res_admm0.1$beta) ``` ``` ## [1] 0.000000000 -0.003938377 0.000000000 0.000000000 0.000000000 ## [6] 0.008219268 ``` --- # Coordinate Descent - Each iteration contains a full cycle of `\(\beta_i\)` updates - Update rule: `$$\beta_{i}\leftarrow\mathcal{S}_{n\lambda/\Vert X_{i}\Vert^{2}}\left(\frac{X_{i}'(y-X_{-i}\beta_{-i})}{\Vert X_{i}\Vert^{2}}\right)$$` - A "cleverer" scheme is to note that `$$\beta_{i}\leftarrow\mathcal{S}_{n\lambda/\Vert X_{i}\Vert^{2}}\left(\beta_i+\frac{X_{i}'r}{\Vert X_{i}\Vert^{2}}\right),\quad r=y-X\beta$$` - Then update `\(r\leftarrow r - (\beta_i^{new} - \beta_i^{old})X_i\)` --- # Implementation ```r # Soft-thresholding function soft_thresh = function(x, a) { sign(x) * pmax(0, abs(x) - a) } init_cd = function(x, y, lam) { xi_square = colSums(x^2) thresh = nrow(x) * lam / xi_square list(xi_square = xi_square, thresh = thresh) } update_cd = function(beta, k, x, y, lam, state) { new_beta = beta # betai <- S(betai + xi' * r / ||xi||^2, t), r = y - x * beta r = y - c(x %*% beta) for(i in seq_along(new_beta)) { old = new_beta[i] newb = old + sum(x[, i] * r) / state$xi_square[i] thresh = state$thresh[i] new_beta[i] = soft_thresh(newb, thresh) r = r - sum(new_beta[i] - old) * x[, i] } list(beta = new_beta, state = state) } ``` --- # Result ```r res_cd = run_opt(x, y, lam, init_cd, update_cd) ``` ``` ## Iter 0, loss = 0.046708 ## Iter 100, loss = 0.027825 ## Iter 200, loss = 0.027825 ## Iter 300, loss = 0.027825 ## Iter 400, loss = 0.027825 ## Iter 500, loss = 0.027825 ## Iter 600, loss = 0.027825 ## Iter 700, loss = 0.027825 ## Iter 800, loss = 0.027825 ## Iter 900, loss = 0.027825 ## Iter 1000, loss = 0.027825 ``` ```r head(res_cd$beta) ``` ``` ## [1] -0.3862278 1.4304117 -0.2206913 1.1256895 0.1704706 0.8657182 ``` ```r tail(res_cd$beta) ``` ``` ## [1] 0.000000000 -0.003938377 0.000000000 0.000000000 0.000000000 ## [6] 0.008219268 ``` --- # Comparison ```r K = 1000 gdat = data.frame( iter = rep(1:K, times = 8), loss = c(res_subgrad1$losses[1:K], res_subgrad10$losses[1:K], res_ista$losses[1:K], res_fista$losses[1:K], res_drs1$losses[1:K], res_drs10$losses[1:K], res_admm1$losses[1:K], res_cd$losses[1:K]), method = rep(c("Subgrad α=1", "Subgrad α=10", "ISTA", "FISTA", "DRS α=1", "DRS α=10", "ADMM ρ=1", "CD"), each = K) ) ``` --- # Comparison ```r library(ggplot2) ggplot(gdat, aes(x = iter, y = log10(loss - obj_opt))) + geom_line(aes(color = method)) + scale_color_hue("Method") + xlab("Iteration") + ylab("Log-error") + theme_bw()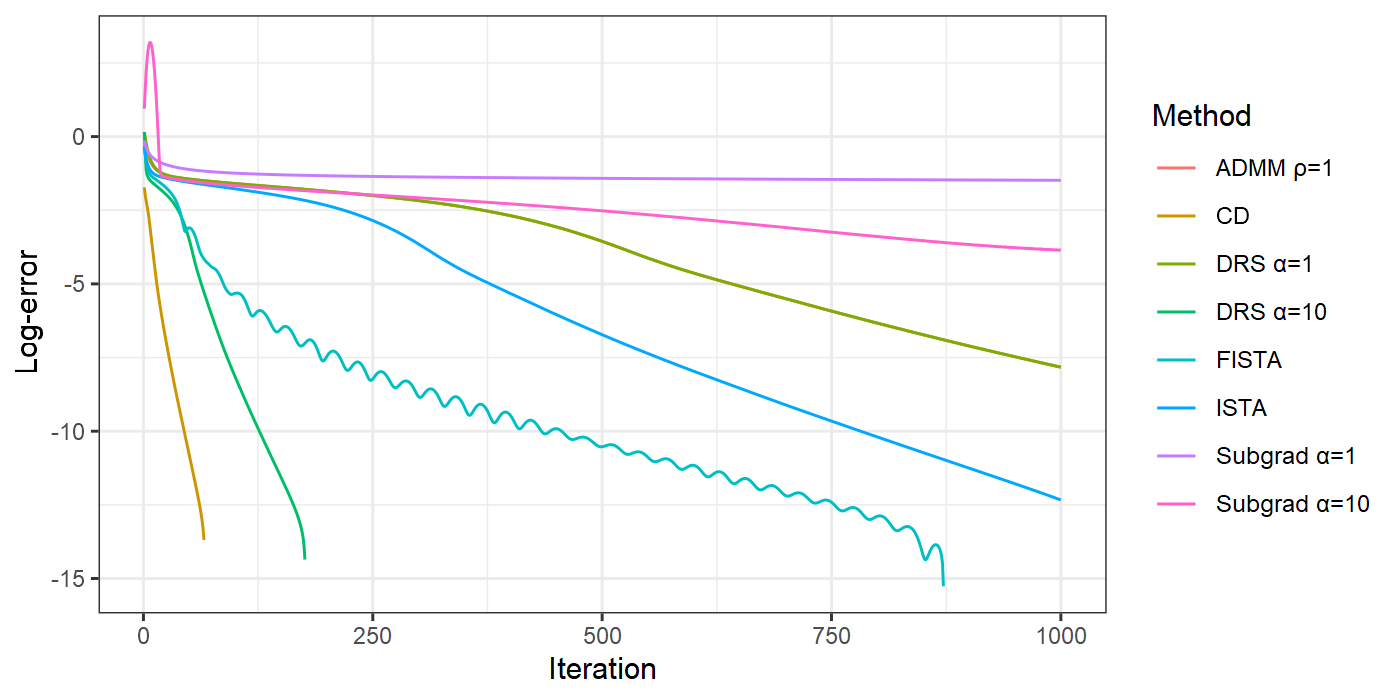 ``` <img src="lec9_files/figure-html/unnamed-chunk-21-1.png" style="display: block; margin: auto;" /> --- # More Considerations The previous comparison is neither rigorous nor complete, and more works need to be done: - The plot only shows error v.s. iteration, but not error v.s. computing time - The direct factorization of `\(A=I+(\alpha/n)X'X\)` is not optimal (recall that `\(p>n\)`) - Design of algorithms when `\(X\)` is sparse (i.e., operating on the `xsp` object) Left as after-class exercises. --- # References .medium[ [1] Stephen Boyd et al. (2011). Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine learning. [2] Deng Wei et al. (2017). Parallel multi-block ADMM with O(1/k) convergence. Journal of Scientific Computing. [3] Paul Tseng (2001). Convergence of a block coordinate descent method for nondifferentiable minimization. Journal of optimization theory and applications. [4] Peter Richtárik and Martin Takáč (2014). Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function. Mathematical Programming. ]