class: center, middle, inverse, title-slide .title[ # Computational Statistics ] .subtitle[ ## Lecture 7 ] .author[ ### Yixuan Qiu ] .date[ ### 2023-10-25 ] --- class: inverse, center, middle # Optimization --- # Today's Topics - Subgradient and subdifferential - Subgradient methods - Proximal gradient descent --- # Last Time - The simplest gradient descent method deals with .highlight[unconstrained and smooth] problems - Projected gradient descent extends it to .highlight[constrained] problems - Today we discuss how to deal with .highlight[nonsmooth] problems --- # 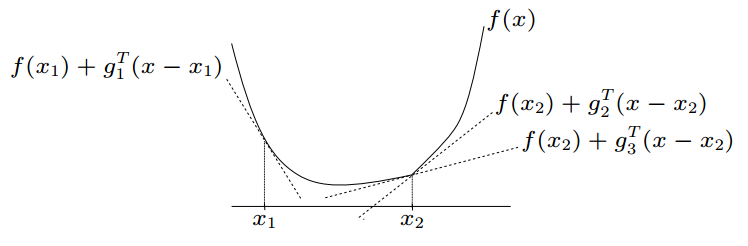Subgradient A subgradient of a convex function `\(f:\mathbb{R}^d\rightarrow\mathbb{R}\)` at a point `\(x\)` is .highlight[any] vector `\(g\in\mathbb{R}^d\)` such that `$$f(y)\ge f(x)+g'(y-x),\quad\forall y\in\mathcal{X},$$` where `\(\mathcal{X}\)` is the domain of `\(f\)`. -- Recall that if `\(f\)` is differentiable, then `\(f\)` is convex if and only if `$$f(y)\ge f(x)+[\nabla f(x)]'(y-x),\quad \forall x,y\in \mathcal{X}.$$` --- # Subdifferential The set of all subgradients of `\(f\)` at `\(x\)` is called the .highlight[subdifferential]: `$$\partial f(x)=\{g\in\mathbb{R}^d:g \text{ is a subgradient of } f \text{ at } x\}.$$` .center[ <img src="images/subgrad.png" /> .small[(Image: https://optimization.mccormick.northwestern.edu/index.php/Subgradient_optimization)] ] --- # Properties - Subgradient always exists for convex functions (subdifferential is nonempty) - `\(\partial f(x)\)` is closed and convex - `\(f\)` is differentiable at `\(x\)` if and only if the subdifferential is a singleton containing the gradient: `\(\partial f(x)=\{\nabla f(x)\}\)` --- # Properties - .highlight[Linear combination]: `\(\partial(\alpha_1 f_1+\alpha_2 f_2)=\alpha_1\cdot\partial f_1+\alpha_2\cdot\partial f_2\)`, where `\(\alpha_1,\alpha_2\ge 0\)`, and for two sets `\(C_1,C_2\)`, `\(\alpha C_1+\beta C_2=\{\alpha x_1+\beta x_2:x_1\in C_1,x_2\in C_2\}\)` - .highlight[Affine transformation]: If `\(g(x)=f(Ax+b)\)`, then `\(\partial g(x)=A'\partial f(Ax+b)\)` - .highlight[Chain rule]: Let `\(f\)` be convex, `\(g\)` be convex, differentiable, and nondecreasing. Denote by `\(h(x)=g(f(x))\)`, and then `\(\partial h(x)=g'(f(x))\partial f(x)\)` --- # Examples For `\(f=\Vert x \Vert\)`: - If `\(x\neq 0\)`, `\(\partial f(x)=\{x/\Vert x\Vert\}\)` - If `\(x=0\)`, `\(\partial f(x)=\{z:\Vert z\Vert\le 1\}\)` For `\(f=\Vert x \Vert_1\)`: - `\(\partial f(x)=\{(g_1,\ldots,g_d)':g_i\in G_i\}\)`, where - If `\(x_i\neq 0\)`, `\(G_i=\{\mathrm{sign}(x_i)\}\)` - If `\(x_i=0\)`, `\(G_i=[-1,1]=\{z:|z|\le 1\}\)` --- # Examples ^{<span class="small">[3,4]</span>} For `\(f(X)=\lambda_\max(X)\)` defined on all symmetric `\(d\times d\)` matrices, let `\(\lambda_1\ge\cdots\ge\lambda_d\)` be the eigenvalues and `\(\gamma_1,\ldots,\gamma_d\)` be the associated eigenvectors. Then `$$\partial f(X)=\{T\in K:(\lambda_1-\lambda_i)\gamma_i'T\gamma_i=0,\ i=2,\ldots,d\},$$` where `\(K=\{T\in\mathbb{R}^d:T'=T,\,T\succeq 0,\,\mathrm{tr}(T)=1\}\)`. Special cases: - If `\(\lambda_1>\lambda_2\)`, then `\(\partial f(X)=\{\nabla f(X)\}=\{\gamma_1\gamma_1'\}\)`. - If `\(\lambda_1=\cdots=\lambda_r>\lambda_{r+1}\)`, then `$$\partial f(X)=\left\{\sum_{i=1}^r w_i\gamma_i\gamma_i':w\in\mathbb{R}^r,w\ge 0,\sum_{i=1}^r w_i=1\right\}.$$` --- # Relation to Optimality Condition There is a very general rule: `\(x^*\)` is an optimal point of `\(f(x)\)` if and only if 0 is a subgradient of `\(f\)` at `\(x^*\)`: `$$f(x^*)=\min_{x}\,f(x)\Leftrightarrow 0\in \partial f(x^*).$$` This is true even for nondifferentiable `\(f\)`. If `\(f\)` is differentiable, then the condition reduces to `$$\nabla f(x^*)=0.$$` --- class: center, middle # Subgradient Methods --- # Subgradient Descent Recall that gradient descent solves `$$\min_x\ f(x),$$` but it requires `\(f\)` to be differentiable. -- Subgradient descent loosens this condition by replacing the gradient with a subgradient: given an initial value `\(x^{(0)}\)`, iterate `$$x^{(k+1)}=x^{(k)}-\alpha_k\cdot g^{(k)},\quad k=0,1,\ldots,$$` where `\(\alpha_k\)` is the step size, and `\(g^{(k)}\in \partial f(x^{(k)})\)` is .highlight[any] subgradient of `\(f\)` at `\(x^{(k)}\)`. --- # Projected Subgradient Descent If the optimization problem is constrained on a closed and non-empty convex set `\(C\)`, then similar to projected gradient descent, we can use the projected subgradient descent method: `$$x^{(k+1)}=P_C\left(x^{(k)}-\alpha_k\cdot g^{(k)}\right),\quad k=0,1,\ldots.$$` --- # Questions - Does (projected) subgradient descent converge? - How fast does it converge? - How to pick `\(\alpha_k\)`? --- # Convergence Analysis - Subgradient descent can be viewed as a special case of projected subgradient descent - Their convergence properties are similar - We show the results of projected subgradient descent for generality --- # A Fundamental Lemma The projected subgradient descent iterations satisfy `$$\small\Vert x^{(k+1)}-x^{*}\Vert^{2}\le\Vert x^{(k)}-x^{*}\Vert^{2}-2\alpha_{k}(f(x^{(k)})-f(x^{*}))+\alpha_{k}^{2}\Vert g^{(k)}\Vert^{2}.$$` -- **Proof:** `$$\small\begin{align*} \Vert x^{(k+1)}-x^{*}\Vert^{2} & =\Vert P_{C}(x^{(k)}-\alpha_{k}g^{(k)})-x^{*}\Vert^{2}\\ & \le\Vert x^{(k)}-\alpha_{k}g^{(k)}-x^{*}\Vert^{2}\quad\text{(projection is nonexpansive)}\\ & =\Vert x^{(k)}-x^{*}\Vert^{2}-2\alpha_{k}(x^{(k)}-x^{*})'g^{(k)}+\alpha_{k}^{2}\Vert g^{(k)}\Vert^{2} \end{align*}$$` Subgradient satisfy `\(f(x^{*})-f(x^{(k)})\ge(x^{*}-x^{(k)})'g^{(k)}\)`, so the lemma holds. --- # Convergence Property Suppose that `\(f:\mathbb{R}^d\rightarrow\mathbb{R}\)` is convex and Lipschitz continuous on `\(C\)` with constant `\(L\)`. Then `$$f(x_{\text{best}}^{(k)})-f(x^*)\le\frac{\Vert x^{(0)}-x^{*}\Vert^{2}+L^{2}\sum_{i=1}^{k}\alpha_{i}^{2}}{2\sum_{i=0}^{k}\alpha_{i}}.$$` For subgradient methods we can no longer guarantee the objective function values to be nonincreasing, so we select the best iterate `\(x_{\text{best}}^{(k)}\)`, defined by `$$f(x_{\text{best}}^{(k)})=\min_{i=0,\ldots,k}\,f(x^{(i)}).$$` --- # Implications - With a fixed step size `\(\alpha_k\equiv\alpha\)`, `$$f(x_{\text{best}}^{(k)})-f(x^*)\le\frac{\Vert x^{(0)}-x^{*}\Vert^{2}}{2\alpha k}+\frac{L^{2}\alpha}{2}.$$` - With a diminishing step size `\(\alpha_k\)` that satisfies `\(\sum_k\alpha_k^2<\infty\)` and `\(\sum_k\alpha_k=\infty\)`, we have `\(f(x_{\text{best}}^{(k)})\rightarrow f(x^*)\)`. - The "best" choice is `\(\alpha_k=O(1/\sqrt{k})\)`, which gives `$$f(x_{\text{best}}^{(k)})-f(x^*)\sim\frac{\Vert x^{(0)}-x^{*}\Vert^{2}+L^{2}\log(k)}{\sqrt{k}}.$$` --- # Proof Applying the fundamental lemma recursively, and we have `$$\small\Vert x^{(k+1)}-x^{*}\Vert^{2}\le\Vert x^{(0)}-x^{*}\Vert^{2}-2\sum_{i=0}^{k}\alpha_{i}(f(x^{(i)})-f(x^{*}))+\sum_{i=0}^{k}\alpha_{i}^{2}\Vert g^{(i)}\Vert^{2}.$$` Rearranging the terms gives `$$\small\begin{align*} 2\sum_{i=0}^{k}\alpha_{i}(f(x^{(i)})-f(x^{*})) & \le\Vert x^{(0)}-x^{*}\Vert^{2}-\Vert x^{(k+1)}-x^{*}\Vert^{2}+\sum_{i=0}^{k}\alpha_{i}^{2}\Vert g^{(i)}\Vert^{2}\\ & \le\Vert x^{(0)}-x^{*}\Vert^{2}+L^{2}\sum_{i=0}^{k}\alpha_{i}^{2}. \end{align*}$$` --- ## Convergence with Strong Convexity ^{<span class="small">[5]</span>} If in addition, `\(f\)` is strongly convex with parameter `\(m>0\)`, then with a step size `\(\alpha_k=2/(m(k+1))\)`, we have `$$f(x_{\text{best}}^{(k)})-f(x^*)\le\frac{2L^{2}}{m}\cdot\frac{1}{k+1}.$$` --- # Summary - Overall, subgradient methods have slower convergence rates than gradient descent counterparts. - If `\(f\)` is Lipschitz continuous, then the optimization error decays at the rate of `\(O(1/\sqrt{k})\)` (gradient descent is `\(O(1/k)\)`). - If `\(f\)` is Lipschitz continuous and strongly convex, then the optimization error decays at the rate of `\(O(1/k)\)` (gradient descent is `\(O(\rho^k)\)`). --- class: center, middle # Proximal Gradient Descent --- # Motivation - Although subgradient methods are very simple and general in solving nonsmooth convex optimization problems - They have undesirable convergence speed - In many statistical models, the nonsmooth function we want to optimize has a special structure: `$$F(x)=f(x)+h(x),$$` where `\(f\)` is convex and smooth, and `\(h\)` is convex but possibly nonsmooth --- # Examples - For the Lasso problem, `\(F(\beta)=f(\beta)+h(\beta)\)`, where `\(f(\beta)=\frac{1}{2}\Vert y-X\beta\Vert^2\)`, and `\(h(\beta)=\lambda\Vert\beta\Vert_1\)` - Constrained problems `\(\min_{x\in C}\,f(x)\)` can also be written as `\(F(x)=f(x)+h(x)\)`, where `$$h(x)=I_C(x)=\begin{cases} 0, & x\in C\\ \infty, & x\notin C \end{cases}.$$` --- # Proximal Gradient Descent The proximal gradient descent algorithm solves `\(\min_x F(x)\)` using the following iteration scheme: given an initial value `\(x^{(0)}\)`, iterate `$$x^{(k+1)}=\mathbf{prox}_{\alpha h}\left(x^{(k)}-\alpha\cdot\nabla f(x^{(k)})\right),\quad k=0,1,\ldots,$$` where `\(\mathbf{prox}_{\alpha h}(\cdot)\)` is the proximal operator (defined later) of `\(h\)` with step size `\(\alpha\)`. --- # Proximal Operator The .highlight[proximal operator] of a convex function `\(h\)` with step size `\(\alpha\)` is defined as `$$\mathbf{prox}_{\alpha h}(x)=\underset{u}{\arg\min}\ \ h(u)+\frac{1}{2\alpha}\Vert u-x\Vert^{2}.$$` - A Strongly convex optimization problem - But has closed form for many `\(h\)` functions --- ## Examples - If `\(h(x)=\Vert x \Vert\)`, then `$$\mathbf{prox}_{\alpha h}(x)=\begin{cases} (1-\alpha/\Vert x\Vert)x, & \Vert x\Vert\ge\alpha\\ 0, & \Vert x\Vert<\alpha \end{cases}.$$` - If `\(h(x)=(1/2)\Vert x \Vert^2\)`, then `\(\mathbf{prox}_{\alpha h}(x)=(1+\alpha)^{-1}x.\)` - If `\(h(x)=(1/2)x'Ax+b'x+c\)`, where `\(A\)` is positive definite, then `$$\mathbf{prox}_{\alpha h}(x)=(I+\alpha A)^{-1}(x-\alpha b).$$` --- ## Examples - If `\(h(x)=\Vert x \Vert_1\)`, then `\(\mathbf{prox}_{\alpha h}(x)=\mathcal{S}_{\alpha}(x)\)`, the soft-thresholding operator, `$$(\mathcal{S}_{\alpha}(x))_{i}=\begin{cases} x_{i}-\alpha, & x_{i}>\alpha\\ 0, & |x_{i}|\le\alpha\\ x_{i}+\alpha, & x_{i}<-\alpha \end{cases}.$$` - If `\(h(x)=I_C(x)\)`, then `\(\mathbf{prox}_{\alpha h}(x)=P_C(x)\)`, the projection operator. -- - .highlight[This means that proximal gradient descent reduces to projected gradient descent if] `\(\require{color}\color{deeppink}h(x)=I_C(x).\)` --- ## Properties ^{<span class="small">[6]</span>} - If `\(h(x)=a\cdot g(x)+b\)`, `\(a>0\)`, then `\(\mathbf{prox}_{\alpha h}(x)=\mathbf{prox}_{a\alpha g}(x)\)` - If `\(h(x)=g(ax+b)\)`, `\(a\neq 0\)`, then `\(\mathbf{prox}_{\alpha h}(x)=\left(\mathbf{prox}_{a^2\alpha g}(ax+b)-b\right)/a\)` - If `\(h(x)=g(x)+a'x+b\)`, then `\(\mathbf{prox}_{\alpha h}(x)=\mathbf{prox}_{\alpha g}(x-a\alpha)\)` - If `\(h(x)=g(x)+(\rho/2)\Vert x-a\Vert^2\)`, then `\(\mathbf{prox}_{\alpha h}(x)=\mathbf{prox}_{\tilde{\alpha }g}((\tilde{\alpha}/\alpha)x-(\rho\tilde{\alpha})a)\)`, where `\(\tilde{\alpha}=\alpha/(1+\alpha\rho)\)` --- # Convergence Property We first present a nice property of the proximal gradient descent algorithm. The proof can be found at [[7]](https://yuxinchen2020.github.io/ele522_optimization/lectures/proximal_gradient.pdf). Suppose `\(f\)` is convex and `\(L\)`-smooth. Take the step size `\(\alpha=1/L\)`, and then `$$F(x^{(k+1)})\le F(x^{(k)}),\quad \Vert x^{(k+1)}-x^*\Vert\le\Vert x^{(k)}-x^*\Vert.$$` --- # Convergence Property ^{<span class="small">[7]</span>} The main convergence theorem: Suppose `\(f\)` is convex and `\(L\)`-smooth. Take the step size `\(\alpha=1/L\)`, and then `$$F(x^{(k)})-F(x^*)\le\frac{L\Vert x^{(0)}-x^*\Vert^2}{2k}.$$` --- ## Convergence with Strong Convexity ^{<span class="small">[7]</span>} If in addition, `\(f\)` is strongly convex with parameter `\(m>0\)`, then with a fixed step size `\(\alpha= 1/L\)`, we have `$$\Vert x^{(k)}-x^*\Vert^2\le\left(1-\frac{m}{L}\right)^k\Vert x^{(0)}-x^*\Vert^2.$$` --- # Summary - Proximal gradient descent matches the convergence rate of gradient descent. - Useful when `\(\mathbf{prox}_{\alpha h}\)` can be efficiently evaluated. - If `\(f\)` is `\(L\)`-smooth, then the optimization error, `\(F(x^{(k)})-F(x^*)\)`, decays at the rate of `\(O(1/k)\)`. - If `\(f\)` is `\(L\)`-smooth and `\(m\)`-strongly-convex, then the optimization error decays exponentially fast at the rate of `\(O(\rho^k)\)`, where `\(\rho=1-m/L\)`. --- class: center, middle # One More Thing... --- # Nesterov Acceleration It turns out that the proximal gradient descent algorithm can be accelerated almost for free, using a somewhat magical technique. The accelerated version: given an initial value `\(x^{(0)}=x^{(-1)}\)`, iterate `$$\require{color}\begin{align*} y^{(k+1)} & =x^{(k)}\textcolor{deeppink}{+\frac{k-1}{k+2}(x^{(k)}-x^{(k-1)})},\\ x^{(k+1)} & =\mathbf{prox}_{\alpha h}\left(y^{(k+1)}-\alpha\cdot\nabla f(y^{(k+1)})\right),\quad k=0,1,\ldots \end{align*}$$` --- # Convergence Property ^{<span class="small">[8]</span>} The accelerated convergence rate: Suppose `\(f\)` is convex and `\(L\)`-smooth. Take the step size `\(\alpha=1/L\)`, and then `$$F(x^{(k)})-F(x^*)\le\frac{2L\Vert x^{(0)}-x^*\Vert^2}{(k+1)^2}.$$` --- ## Convergence with Strong Convexity ^{<span class="small">[8]</span>} If in addition, `\(f\)` is strongly convex with parameter `\(m>0\)`, then with `\(\kappa=L/m\)`, the iteration becomes `$$\require{color}\begin{align*} y^{(k+1)} & =x^{(k)}\textcolor{deeppink}{+\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}(x^{(k)}-x^{(k-1)})},\\ x^{(k+1)} & =\mathbf{prox}_{\alpha h}\left(y^{(k+1)}-\alpha\cdot\nabla f(y^{(k+1)})\right),\quad k=0,1,\ldots \end{align*}$$` With a fixed step size `\(\alpha= 1/L\)`, we have `$$\small F(x^{(k)})-F(x^{*})\le\left(1-\frac{1}{\sqrt{\kappa}}\right)^{k}\left(F(x^{(0)})-F(x^{*})+\frac{m\Vert x^{(0)}-x^{*}\Vert^{2}}{2}\right).$$` --- # Summary - (Projected) subgradient descent is a general method to optimize a nonsmooth convex function - However, its convergence is typically slow - If the nonsmooth part has a simple proximal operator, then the proximal gradient descent algorithm is much preferred - Also get accelerations "for free" --- # References .medium[ [1] Stephen Boyd and Lieven Vandenberghe (2004). Convex optimization. Cambridge University Press. [2] Robert M. Gower (2018). Convergence theorems for gradient descent. Lecture notes for Statistical Optimization. [3] Claude Vallee, Danielle Fortune, and Camelia Lerintiu (2008). Subdifferential of the Largest Eigenvalue of a Symmetrical Matrix Application of Direct Projection Methods. Analysis and Applications. [4] Adrian S. Lewis (1999). Nonsmooth analysis of eigenvalues. Mathematical Programming. [5] [https://yuxinchen2020.github.io/ele522_optimization/lectures](https://yuxinchen2020.github.io/ele522_optimization/lectures/subgradient_methods.pdf) [/subgradient_methods.pdf](https://yuxinchen2020.github.io/ele522_optimization/lectures/subgradient_methods.pdf) [6] Neal Parikh and Stephen Boyd (2014). Proximal algorithms. Foundations and trends® in Optimization. ] --- # References .medium[ [7] [https://yuxinchen2020.github.io/ele522_optimization/lectures](https://yuxinchen2020.github.io/ele522_optimization/lectures/proximal_gradient.pdf) [/proximal_gradient.pdf](https://yuxinchen2020.github.io/ele522_optimization/lectures/proximal_gradient.pdf) [8] [https://yuxinchen2020.github.io/ele522_optimization/lectures](https://yuxinchen2020.github.io/ele522_optimization/lectures/accelerated_gradient.pdf) [/accelerated_gradient.pdf](https://yuxinchen2020.github.io/ele522_optimization/lectures/accelerated_gradient.pdf) ]