class: center, middle, inverse, title-slide .title[ # Computational Statistics ] .subtitle[ ## Lecture 4 ] .author[ ### Yixuan Qiu ] .date[ ### 2023-09-27 ] --- class: inverse, center, middle # Numerical Linear Algebra --- # Today's Topics - Conjugate gradient method - Eigenvalue computation --- class: center, middle # Conjugate Gradient Method --- # Direct Methods - All the methods introduced so far can be categorized as .highlight[direct methods] to solve linear systems - Meaning that the .highlight[exact] solution to `\(Ax=b\)` can be computed within a finite number of operations (in exact arithmetic) - .highlight[Cons: too expensive to handle very large linear systems] --- # Iterative Methods - Computes a sequence of approximate solutions `\(x^{(k)}\)` that converges to the exact solution - Stops when the precision is sufficient - .highlight[Do not request more precision than is needed] - In each iteration, the computation is typically cheap, e.g., matrix-vector multiplication `\(v\rightarrow Av\)` - .highlight[Especially efficient for sparse matrices] --- # Conjugate Gradient Method - Conjugate gradient method (CG) is a very special linear system solver - .highlight[It is a direct method used as an iterative one] - Aims to solve the linear system `\(Ax=b\)` when `\(A\)` is .highlight[positive definite] (p.d.) --- # Conjugate Gradient Method - Only uses the matrix-vector multiplication `\(v\rightarrow Av\)` - Obtains the exact solution after `\(n\)` steps - Converges fast under some conditions --- # Algorithm ^{<span class="small">[2]</span>}  --- # Convergence ^{<span class="small">[2]</span>} In exact arithmetic, the algorithm converges to the solution of the linear system `\(Ax=b\)` in at most `\(n\)` iterations. --- # Convergence ^{<span class="small">[2]</span>} Let `\(A\)` be a p.d. matrix and denote by `\(x^*\)` the solution to `\(Ax=b\)`. Let `\(x^{(k)}\)` be the sequence of approximate solutions produced by the conjugate gradient method. Then `$$\Vert x^{(k)}-x^*\Vert_2\le 2\sqrt{\kappa}\left(\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}\right)^k\Vert x_0-x^*\Vert_2,$$` where `\(\kappa\)` is the condition number of `\(A\)` (defined later). --- # Condition Number - For any matrix `\(A\)`, the condition number `\(\kappa(A)\)` is defined as `\(\kappa(A)=\mu_{\max}(A)/\mu_{\min}(A)\)`, where `\(\mu_{\max}\)` and `\(\mu_{\min}\)` are the largest and smallest singular values, respectively - For a p.d. matrix `\(A\)`, `\(\kappa(A)=\lambda_{\max}(A)/\lambda_{\min}(A)\)`, where `\(\lambda_{\max}\)` and `\(\lambda_{\min}\)` are the largest and smallest eigenvalues, respectively - `\(\kappa(A)\ge 1\)` - For any .highlight[orthogonal matrix] `\(Q\)`, `\(\kappa(Q)=1\)` and `\(\kappa(QA)=\kappa(AQ)=\kappa(A)\)` --- # Insights - We say a matrix `\(A\)` is .highlight[well-conditioned] if `\(\kappa(A)\)` is small (i.e., `\(\kappa(A)\approx 1\)`) - Otherwise we say `\(A\)` is .highlight[ill-conditioned] (i.e., `\(\kappa(A)\gg 1\)`) - If a p.d. matrix `\(A\)` has almost equal eigenvalues, then `\(\kappa(A)\approx 1\)` and `$$\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}+1}\approx 0.$$` CG will have extremely fast convergence - If `\(A\)` almost loses positive definiteness, `\(\lambda_{\min}(A)\approx 0\)`, then `\(\kappa(A)\gg 1\)`, and CG almost has no progress --- # Implementation - A direct "translation" of the algorithm gives ```r cg = function(A, b, x0 = rep(0, length(b)), eps = 1e-6) { m = length(b) x = x0 p = r = b - A %*% x r2 = sum(r^2) errs = c() for(i in 1:m) { Ap = A %*% p alpha = r2 / sum(p * Ap) x = x + alpha * p r = r - alpha * Ap r2_new = sum(r^2) err = sqrt(r2_new) errs = c(errs, err) if(err < eps) break beta = r2_new / r2 p = r + beta * p r2 = r2_new } list(x = x, errs = errs, niter = i) } ``` --- # Implementation - We test on a simulated matrix - However, the algorithm does not seem to converge, and the error is quite large ```r set.seed(123) n = 100 M = matrix(0.1 * rnorm(n^2), n) A = crossprod(M) b = rnorm(n) sol = cg(A, b, eps = 1e-12) sol$niter ``` ``` ## [1] 100 ``` ```r max(abs(A %*% sol$x - b)) ``` ``` ## [1] 0.5763024 ``` --- # Implementation - We can find that `\(A\)` is ill-conditioned ```r kappa(A) ``` ``` ## [1] 1164091 ``` - Adding a positive number to the diagonal results in much smaller condition number ```r kappa(A1 <- A + diag(rep(0.1, n))) ``` ``` ## [1] 134.8415 ``` ```r kappa(A2 <- A + diag(rep(1, n))) ``` ``` ## [1] 15.01074 ``` --- # Implementation ```r sol1 = cg(A1, b, eps = 1e-12) sol1$niter ``` ``` ## [1] 78 ``` ```r max(abs(A1 %*% sol1$x - b)) ``` ``` ## [1] 1.588243e-13 ``` ```r sol2 = cg(A2, b, eps = 1e-12) sol2$niter ``` ``` ## [1] 29 ``` ```r max(abs(A2 %*% sol2$x - b)) ``` ``` ## [1] 1.858513e-13 ``` --- # Implementation - Plot the residual norms (in log-scale) against iterations <img src="lec4_files/figure-html/unnamed-chunk-6-1.png" width="80%" style="display: block; margin: auto;" /> --- # 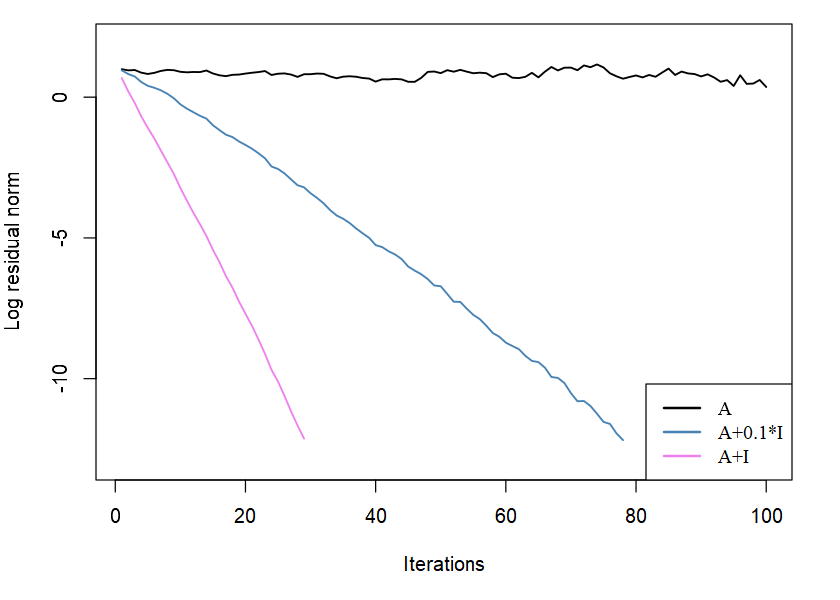Implementation - We will see a more useful example when we consider linear regression on sparse matrices --- # When to Use - `\(A\)` is p.d. and is well-conditioned - The matrix-vector operation `\(v\rightarrow Av\)` is cheap - One example is sparse matrix, or product of sparse matrices - We will elaborate this point when we study sparse matrices --- class: center, middle # Eigenvalue Computation --- # Eigenvalues - Eigenvalues are important characteristics of matrices - Wide applications in statistics, e.g., principal component analysis (PCA), spectral clustering, matrix norm, random matrix theory, etc. - Eigenvalue computation is one of the core topics of numerical linear algebra --- # Definition - The definition of eigenvalue is actually quite simple - For a square matrix `\(A\)`, we call the solution `\(\lambda\)` to the equation `\(Ax=\lambda x\)` an eigenvalue of `\(A\)` - The corresponding `\(x\)` vector is an eigenvector - Here we focus on .highlight[real symmetric matrices] --- # Decomposition Theorem ^{<span class="small">[2]</span>} A matrix `\(A_{n\times n}\)` is real symmetric if and only if there exists a real orthogonal matrix `\(\Gamma\)` and real eigenvalues `\(\lambda_1,\ldots,\lambda_n\)` such that `$$A=\Gamma D\Gamma',$$` where `\(D=\mathrm{diag}(\lambda_1,\ldots,\lambda_n)\)`. This is typically called the .highlight[eigenvalue decomposition], or .highlight[spectral decomposition], of `\(A\)`. --- # Basic Properties Suppose that `\(A\)` is a real symmetric matrix - `\(A\)` is p.d. if all its eigenvalues are strictly positive - `\(A^k=\Gamma D^k\Gamma'\)`, `\(k=\ldots,-2,-1,0,1,2,\ldots\)` - `\(\det(A)=\lambda_1\cdots\lambda_n\)` - `\(\mathrm{tr}(A)=\lambda_1+\cdots+\lambda_n\)` --- # Basic Properties - Min-Max principle `$$\lambda_{\min}(A)=\underset{x\neq 0}{\min}\frac{x'Ax}{x'x}=\underset{\Vert x\Vert=1}{\min}\ x'Ax$$` `$$\lambda_{\max}(A)=\underset{x\neq 0}{\max}\frac{x'Ax}{x'x}=\underset{\Vert x\Vert=1}{\max}\ x'Ax$$` - This gives PCA a nice interpretation: the first principal component maximizes the explained variance --- # Computing Eigenvalues There are different cases of computing eigenvalues - Computing all eigenvalues (eigenvalue decomposition) - Computing the largest eigenvalue - Computing the eigenvalue that is closest to a given number - ... --- # Computing Eigenvalues - Eigenvalue computation is a large field in numerical linear algebra - The actual algorithms used in practice are usually quite involved - For the purpose of statistical computing, we mainly introduce the basic ideas behind these algorithms and some recommended implementations - In what follows, we focus on finding eigenvalues of real symmetric matrices --- class: center, middle # All Eigenvalues --- # Computing All Eigenvalues The most commonly-used method to compute all eigenvalues consists of two steps: 1. Looking for an orthogonal matrix `\(Q\)` such that `\(Q'AQ\)` is tridiagonal `$$Q'AQ=T=\begin{bmatrix}\alpha_{1} & \beta_{2}\\ \beta_{2} & \alpha_{2} & \beta_{3}\\ & \ddots & \ddots & \ddots\\ & & \beta_{n-1} & \alpha_{n-1} & \beta_{n}\\ & & & \beta_{n} & \alpha_{n} \end{bmatrix}$$` 2. Applying the QR algorithm (introduced later) to the matrix `\(T\)` to compute all eigenvalues --- # The Householder (Tridiagonalization) Algorithm - The Householder algorithm finds a sequence of (simple) orthogonal matrices `\(Q_k\)` such that `$$T=(Q_1\cdots Q_{n-2})'A(Q_1\cdots Q_{n-2}),$$` where `\(T\)` is tridiagonal - `\(Q=Q_1\cdots Q_{n-2}\)` is also orthogonal (why?) - `\(A\)` and `\(T\)` have the same eigenvalues (why?) - The motivation is that `\(T\)` has cheaper matrix operations --- # The Householder (Tridiagonalization) Algorithm - A very nice intro orthogonal transformatioduction to the Householder algorithm can be found at Section 4.3 and Section 4.6.1 of https://people.inf.ethz.ch/arbenz/ewp/Lnotes/chapter4.pdf --- # The QR Algorithm The QR algorithm iteratively reduces the tridiagonal `\(T\)` into a diagonal matrix by orthogonal transformations: 1. Initialize `\(T^{(0)}=T\)`, and begin the loop `\(k=0,1,\ldots\)` 2. Compute the QR decomposition of the matrix `\(T^{(k)}\)`: `$$T^{(k)}=Q_k R_k$$` 3. Update `\(T^{(k+1)}=R_k Q_k=Q_k'T^{(k)}Q_k\)` Assume that `\(|\lambda_1|>\cdots>|\lambda_n|>0\)`, and then `\(T^{(k)}\)` converges to a diagonal matrix, whose diagonal elements are eigenvalues of `\(T\)` and `\(A\)`. --- # Practical Algorithm - The lower triangular elements `\(T_{ij}^{(k)}\)`, `\(i>j\)` converge to zero at the rate of `\(O(|\lambda_i/\lambda_j|)\)` ^{<span class="small">[2]</span>} - To accelerate the convergence, a shift can be applied to the original matrix: 1. Compute the QR decomposition of the shifted matrix, `$$T^{(k)}-\sigma_k I_n=Q_k R_k$$` 2. Update `\(T^{(k+1)}=R_k Q_k+\sigma_k I_n=Q_k'T^{(k)}Q_k\)` - We can take `\(\sigma_k=(T^{(k)})_{nn}\)` until `\(T_{n-1,n}^{(k)}\approx 0\)`, and then switch to `\(\sigma_k=(T^{(k)})_{n-1,n-1}\)` --- # Complexity - The Householder algorithm costs `\(O(n^3)\)` - The QR decomposition of tridiagonal matrices has a specialized algorithm, which costs `\(O(n^2)\)` instead of `\(O(n^3)\)` (the latter for general dense matrices) - It can be proved that all `\(T^{(k)}\)` matrices are tridiagonal - The number of iterations required in the QR algorithm depends on the distribution of eigenvalues --- class: center, middle # Largest Eigenvalue --- # Computing the Largest Eigenvalue - In many applications, we only need the largest eigenvalue (in absolute value) - It can be extended to computing the largest `\(k\)` eigenvalues - If `\(\lambda_1,\ldots,\lambda_n\)` are eigenvalues of `\(A\)` with `\(|\lambda_1|>\cdots>|\lambda_n|\)`, and `\(\gamma_1,\ldots,\gamma_n\)` are the associated eigenvectors, then: - `\(\lambda_2\)` is the largest eigenvalue of `\(A-\lambda_1\gamma_1\gamma_1'\)` - `\(\lambda_3\)` is the largest eigenvalue of `\(A-\lambda_1\gamma_1\gamma_1'-\lambda_2\gamma_2\gamma_2'\)` - ... --- # Power Method ^{<span class="small">[2]</span>} One widely-used and possibly the simplest method to compute the largest eigenvalue (in absolute value) is the power method  --- # Convergence ^{<span class="small">[2]</span>} Assume `\(A\)` has eigenvalues `\(\lambda_1>|\lambda_2|\ge\cdots\ge|\lambda_n|\)` and associated eigenvectors `\(\gamma_1,\ldots,\gamma_n\)`. Also assume the initial vector satisfies `\(x_0=\sum_{i=1}^n\beta_i\gamma_i\)` for some `\(\beta_1\neq 0\)`. Then `$$\left|\Vert y_{k}\Vert-\lambda_{1}\right|\le C\left(\frac{|\lambda_{2}|}{\lambda_{1}}\right)^{k},\qquad\Vert x_{k}-\tilde{\gamma}_{1}\Vert\le C\left(\frac{|\lambda_{2}|}{\lambda_{1}}\right)^{k},$$` where `\(\tilde{\gamma_1}=\pm\gamma_1\)`. --- # Pros and Cons - The power method only requires the matrix-vector multiplication `\(v\rightarrow Av\)` to compute eigenvalues of `\(A\)` (recall the CG method) - This is important and useful for sparse matrices - However, it does not effectively use the information of past iterations - Also, it can only compute one eigenvalue at one time --- # Advanced Algorithms - Mainstream software packages typically use other advanced algorithms to compute the largest eigenvalues, e.g., - .highlight[Implicitly restarted Lanczos method] ^{<span class="small">[4]</span>} - .highlight[Jacobi–Davidson algorithm] ^{<span class="small">[5]</span>} - They also only need the `\(v\rightarrow Av\)` operation - Can compute multiple eigenvalues together - These algorithms themselves are quite sophisticated, however --- class: center, middle # Eigenvalue Closest to `\(\mu\)` --- # Computing Eigenvalue Closest to `\(\mu\)` - Another type of problem is to find the eigenvalue that is closest to a given number `\(\mu\)` - For example, if `\(\mu=0\)`, then this is equivalent to finding the smallest eigenvalue (in absolute value) - Fortunately, we can make use of existing methods that compute largest eigenvalues for this task, via a technique called .highlight[spectral transformation] --- # Spectral Transformation Spectral transformation is based on the following finding. If `\(\lambda_i\)`, `\(i=1,\ldots,n\)` are eigenvalues of `\(A\)`, then `\(Ax_i=\lambda_i x_i\)` for the eigenvectors `\(x_i\)`. Choose a shift `\(\mu\neq\lambda_i\)`, then the eigenvalues of `\(B=(A-\mu I_n)^{-1}\)` are `\(\theta_i=(\lambda_i-\mu)^{-1}\)`, and `\(B x_i=\theta_i x_i\)`. Therefore, the largest eigenvalue of `\(B\)` corresponds to the eigenvalue of `\(A\)` that is closest to `\(\mu\)`. --- # Inverse Iteration - If we want to compute the eigenvalue of `\(A\)` closest to `\(\mu\)` - We can apply the power method (or other methods based on matrix-vector multiplication) to `\(B=(A-\mu I_n)^{-1}\)` - The iteration becomes `$$\begin{align*} y_{k} & =(A-\mu I_{n})^{-1}x_{k-1}\\ x_{k} & =y_{k}/\Vert y_{k}\Vert \end{align*}$$` - By the convergence theorem, we have `\(\Vert y_k \Vert\rightarrow \theta_1\)` - Then recover the eigenvalue of `\(A\)` by `\(\lambda_\mu=\mu+1/\theta_1\)` --- # Solving Linear Systems - In actual implementation, we do not directly compute the matrix inverse `\((A-\mu I_{n})^{-1}\)` - Instead, we factorize `\(A-\mu I_{n}\)` once using LU decomposition or `\(LDL^T\)` decomposition - And then solve the linear systems `\((A-\mu I_n)y_k=x_{k-1}\)` --- # Implementation - The `eigen()` function in base R is a very stable and efficient function to compute .highlight[all eigenvalues] - Specify `symmetric = TRUE` if you know your matrix is symmetric (by default it will detect symmetry) - Specify `only.values = TRUE` if you do not need eigenvectors --- # Benchmark ```r library(dplyr) set.seed(123) n = 1000 M = matrix(rnorm(n^2), n) A = M + t(M) bench::mark( eigen(A), eigen(A, symmetric = FALSE), eigen(A, symmetric = TRUE), eigen(A, symmetric = TRUE, only.values = TRUE), min_iterations = 3, max_iterations = 10, check = FALSE ) %>% select(expression, min, median) ``` ``` ## # A tibble: 4 × 3 ## expression min median ## <bch:expr> <bch:tm> <bch:tm> ## 1 eigen(A) 1.22s 1.22s ## 2 eigen(A, symmetric = FALSE) 4.32s 4.34s ## 3 eigen(A, symmetric = TRUE) 1.18s 1.19s ## 4 eigen(A, symmetric = TRUE, only.values = TRUE) 326.67ms 330.35ms ``` --- # Implementation - To compute a subset of eigenvalues up to some selection rule, we have several options - The **RSpectra** package implements the implicitly restarted Lanczos method - The **PRIMME** package uses the Jacobi-Davidson algorithm - The **irlba** package is designed for singular value decomposition (next class), but can also be used to compute the largest eigenvalues - My personal favorite is the **RSpectra** package (this is a highly biased choice, of course) --- # Implementation - The code below computes three eigenvalues with largest absolute values ```r library(RSpectra) e = eigs_sym(A, k = 3, which = "LM") e$values ``` ``` ## [1] 88.83776 88.31500 -88.98945 ``` ```r head(e$vectors) ``` ``` ## [,1] [,2] [,3] ## [1,] 0.01506291 0.029602478 -0.015855700 ## [2,] -0.05124211 0.016404205 -0.014749483 ## [3,] -0.01542738 -0.002350839 0.005520141 ## [4,] 0.02921002 -0.006653817 -0.003387408 ## [5,] -0.02406133 0.039802584 0.028103112 ## [6,] -0.01309102 -0.026105929 0.073813795 ``` --- # Implementation - If you want the largest three eigenvalues without taking absolute values, use `which = "LA"` ```r e = eigs_sym(A, k = 3, which = "LA") e$values ``` ``` ## [1] 88.83776 88.31500 87.18646 ``` - If no eigenvectors are needed, add the following option ```r e = eigs_sym(A, k = 3, which = "LA", opts = list(retvec = FALSE)) e$vectors ``` ``` ## NULL ``` --- # Benchmark - If only part of the eigenvalues are needed, `eigs_sym()` is much faster than `eigen()` ```r bench::mark( eigen(A, symmetric = TRUE), eigen(A, symmetric = TRUE, only.values = TRUE), eigs_sym(A, k = 3, which = "LM"), eigs_sym(A, k = 3, which = "LM", opts = list(retvec = FALSE)), min_iterations = 3, max_iterations = 10, check = FALSE ) %>% select(min, median) ``` ``` ## # A tibble: 4 × 2 ## min median ## <bch:tm> <bch:tm> ## 1 1.2s 1.2s ## 2 330.7ms 335.7ms ## 3 158.8ms 159.2ms ## 4 157.1ms 159.3ms ``` - The difference will be more evident on sparse matrices (next class) --- # Implementation - If one needs the smallest three eigenvalues (in absolute value) ```r e = eigs_sym(A, k = 3, which = "LM", sigma = 0) e$values ``` ``` ## [1] 0.01589015 -0.14248784 -0.26307129 ``` - In general, if `sigma` is not `NULL`, then the selection rule is applied to `\(1/(\lambda_i-\sigma)\)` - This only affects the selection rule - The returned eigenvalues are still for `\(A\)` --- # References .medium[ [1] Folkmar Bornemann (2018). Numerical Linear Algebra. Springer. [2] Grégoire Allaire and Sidi Mahmoud Kaber (2008). Numerical linear algebra. Springer. [3] Åke Björck (2015). Numerical methods in matrix computations. Springer. [4] Danny C. Sorensen (1997). Implicitly restarted Arnoldi/Lanczos methods for large scale eigenvalue calculations. In Parallel Numerical Algorithms (pp. 119-165). Springer. [5] Gerard L.G. Sleijpen and Henk A. Van der Vorst (1996). A Jacobi–Davidson iteration method for linear eigenvalue problems. SIAM Journal on Matrix Analysis and Applications, 17(2), 401-425. ]