Computational Statistics
Lecture 3
Yixuan Qiu
2023-09-20
1 / 54

Numerical Linear Algebra2 / 54

Today's Topics

Case studies
- Spline fitting
- Back to regression
New topics
- $L D L^{T}$ decomposition
- QR decomposition

3 / 54

Spline Fitting4 / 54

Interpolation Problem

Given observed points $x = (x_{0}, \dots, x_{n})^{'}$ and $y = (y_{0}, \dots, y_{n})^{'}$ , find a function $f (x)$ such that $f (x_{i}) = y_{i}, i = 0, \dots, n$ .

5 / 54

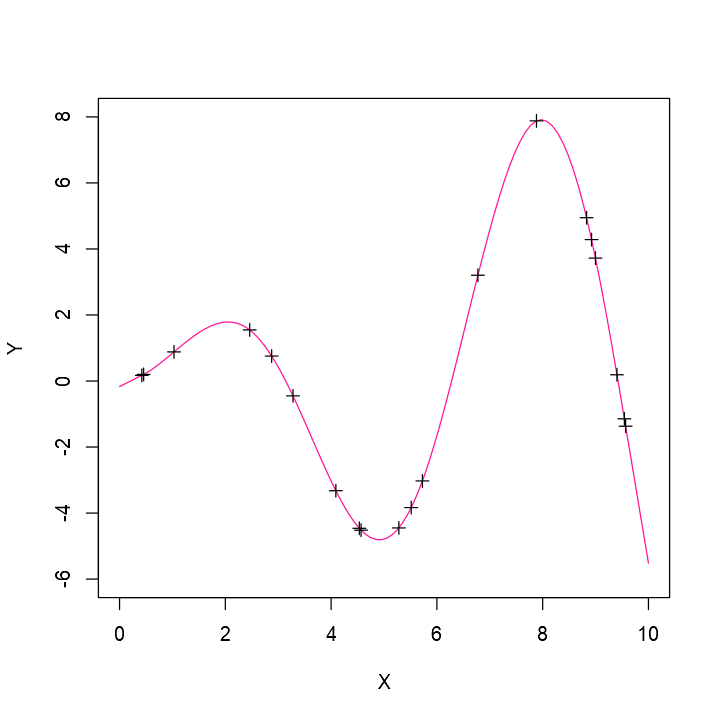
Spline Fitting

Without loss of generality we can assume that $x_{0} < x_{1} < \dots < x_{n}$
We typically require that $f$ is continuous, or differentiable, or smooth (2nd derivative exists)
One important class of functions commonly used for interpolation are piecewise polynomials, also known as spline functions
Spline fitting is the task of determining polynomial coefficients in each interval

6 / 54

Natural Cubic Spline

A commonly-used spline is the natural cubic spline
Has continuous second derivative
On each interval $[x_{i}, x_{i + 1}]$ , it is a cubic polynomial $f (x) = f_{i} (x) = a_{i} + b_{i} (x - x_{i}) + c_{i} (x - x_{i})^{2} + d_{i} (x - x_{i})^{3}$
We need to determine the coefficients $(a_{i}, b_{i}, c_{i}, d_{i})$ , $i = 0, \dots, n - 1$

7 / 54

Natural Cubic SplineNatural cubic splines must satisfy some constraints
Interpolating observed pointsf0(x0)=y0f0(x0)=y0
fi−1(xi)=fi(xi)=yifi−1(xi)=fi(xi)=yi, i=1,…,n−1i=1,…,n−1
fn−1(xn)=ynfn−1(xn)=yn

Continuous first derivativef′i−1(xi)=f′i(xi)fi−1′(xi)=fi′(xi), i=1,…,n−1i=1,…,n−1

Continuous second derivativef′′i−1(xi)=f′′i(xi)fi−1″(xi)=fi″(xi), i=1,…,n−1i=1,…,n−1

Zero second derivative at end pointsf′′0(x0)=f′′n−1(xn)=0f0″(x0)=fn−1″(xn)=0

8 / 54

Theorem

The natural cubic spline that satisfies the conditions in the previous slide has the form

$\begin{aligned} f_{i} (x) & = \frac{z_{i + 1} (x - x_{i})^{3} + z_{i} (x_{i + 1} - x)^{3}}{6 h_{i}} \\ + (\frac{y_{i + 1}}{h_{i}} - \frac{z_{i + 1} h_{i}}{6}) (x - x_{i}) \\ + (\frac{y_{i}}{h_{i}} - \frac{z_{i} h_{i}}{6}) (x_{i + 1} - x), i = 0, \dots, n - 1 \end{aligned}$ where $h_{i} = x_{i + 1} - x_{i}$ , and $z_{i} = f^{″} (x_{i})$ are values to be determined

9 / 54

Spline Fitting

We have assume that $z_{0} = z_{n} = 0$
So there are $(n - 1)$ unknown values $z_{1}, \dots, z_{n - 1}$
The relation $f_{i - 1}^{'} (x_{i}) = f_{i}^{'} (x_{i})$ , $i = 1, \dots, n - 1$ gives $6 (b_{i} - b_{i - 1}) = h_{i - 1} z_{i - 1} + 2 (h_{i - 1} + h_{i}) z_{i} + h_{i} z_{i + 1},$ where $b_{i} = (y_{i + 1} - y_{i}) / h_{i}$

10 / 54

Spline Fitting

Further let $v_{i} = 2 (h_{i - 1} + h_{i})$ , $u_{i} = 6 (b_{i} - b_{i - 1})$
Then we get a tridiagonal system

$[\begin{matrix} v_{1} & h_{1} \\ h_{1} & v_{2} & h_{2} \\ h_{2} & v_{3} & ⋱ \\ ⋱ & ⋱ & h_{n - 2} \\ h_{n - 2} & v_{n - 1} \end{matrix}] [\begin{matrix} z_{1} \\ z_{2} \\ z_{3} \\ ⋮ \\ z_{n - 1} \end{matrix}] = [\begin{matrix} u_{1} \\ u_{2} \\ u_{3} \\ ⋮ \\ u_{n - 1} \end{matrix}]$

Solving the system gives the expression of the spline function

11 / 54

Back to Regression12 / 54

Computing predicted values of linear regression $\hat{y} = X (X^{'} X)^{- 1} X^{'} Y$ .
NEVER do the following:

X %*% solve(t(X) %*% X) %*% t(X) %*% Y

Benchmark

set.seed(123)
X = matrix(rnorm(5000 * 500), 5000)
Y = rnorm(5000)
system.time(X %*% solve(t(X) %*% X) %*% t(X) %*% Y)

##    user  system elapsed 
##    9.09    0.03    9.36

What's wrong with this implementation?

13 / 54

First improvement

Let's first try a simple "magic"

system.time(X %*% (solve(t(X) %*% X) %*% (t(X) %*% Y)))

##    user  system elapsed 
##    0.91    0.00    0.93

Recall the previous implementation

X %*% solve(t(X) %*% X) %*% t(X) %*% Y

You get ~10x speedup almost for free
The only differences are two pairs of parentheses!

14 / 54

Principle 1

When multiplying several matrices together, prefer to first compute the product involving smaller matrices
Reason: the computational complexity of the matrix multiplication $A_{m \times n} B_{n \times p}$ is $O (m n p)$

15 / 54

Second improvement

system.time(X %*% solve(t(X) %*% X, t(X) %*% Y))

##    user  system elapsed 
##    0.78    0.00    0.76

16 / 54

Principle 2

Avoid explicit matrix inversion whenever possible
Instead, solve linear systems
In fact, in statistical computing, it is very rare that you really need $A^{- 1}$
Computing $A^{- 1} B$ is equivalent to solving $A X = B$
Computing $B A^{- 1}$ is equivalent to solving $A^{'} X = B^{'}$

17 / 54

Third improvement

system.time(X %*% solve(crossprod(X), crossprod(X, Y)))

##    user  system elapsed 
##    0.72    0.00    0.70

18 / 54

Principle 3

Avoid explicit matrix transpose
Try specialized functions
crossprod(x): compute $X^{'} X$
crossprod(x, y): compute $X^{'} Y$
tcrossprod(x, y): compute $X Y^{'}$

19 / 54

Principle 4

Utilize special structures of matrices
For example, symmetry, positive definiteness, etc.
Try to further improve the solution!

20 / 54

LDLTLDLT Decomposition21 / 54

Motivation

LU decomposition applies to general square matrices
Cholesky decomposition applies to positive definite matrices
- Halves the storage cost
- Typically faster than LU decomposition
If we only know the matrix is symmetric
Is there any tailored decomposition method?

22 / 54

$L D L^{T}$ Decomposition

[4] shows that a nonsingular symmetric matrix $A$ can be decomposed as $A = L D L^{'}$
$L$ is lower triangular with ones on the diagonal
$D$ is a block diagonal matrix, each block being $1 \times 1$ or $2 \times 2$ , e.g.,

$[\begin{matrix} \begin{array}{rrrrr} 1 & - 3 & 4 & - 4 & 0 \\ - 3 & 10 & - 12 & 6 & 13 \\ 4 & - 12 & 11 & - 1 & - 25 \\ - 4 & 6 & - 1 & 6 & - 5 \\ 0 & 13 & - 25 & 5 & 42 \end{array} \end{matrix}] = [\begin{matrix} \begin{array}{rrrrr} 1 \\ - 3 & 1 \\ 4 & - 2 & 1 \\ - 4 & 0 & - 3 & 1 \\ 0 & 3 & 5 & 2 & 1 \end{array} \end{matrix}] [\begin{matrix} \begin{array}{rrrrr} 1 \\ 1 & 2 \\ 2 & - 1 \\ - 1 \\ 2 \end{array} \end{matrix}] [\begin{matrix} \begin{array}{rrrrr} 1 & - 3 & 4 & - 4 & 0 \\ 1 & - 2 & 0 & 3 \\ 1 & - 3 & 5 \\ 1 & 2 \\ 1 \end{array} \end{matrix}]$

In practice, a permutation matrix would be applied to $A$ for factorization, i.e., $P^{'} A P = L D L^{'}$

23 / 54

Solving Linear Systems

Suppose the decomposition $P^{'} A P = L D L^{'}$ is given
If we wish to solve $A x = b$ , then:

Compute $\tilde{b} = P^{'} b$
Solve $L y_{1} = \tilde{b}$ to get $y_{1}$
Solve $D y_{2} = y_{1}$ to get $y_{2}$
Solve $L^{'} \tilde{x} = y_{2}$ to get $\tilde{x}$
Compute $x = P \tilde{x}$

24 / 54

Solving Linear Systems

Solving $D y = c$ is similar to solving a diagonal system
Since $D$ is block diagonal, $D = b d i a g (D_{1}, \dots, D_{K})$
Each $D_{k}$ is $1 \times 1$ or $2 \times 2$
Partition $c$ according to $D$ , $c = (c_{1}^{'}, \dots, c_{K}^{'})^{'}$
Then $y = ((D_{1}^{- 1} c_{1})^{'}, \dots, (D_{K}^{- 1} c_{K})^{'})^{'}$
If $D_{k}$ is $2 \times 2$ , use closed-form inverse formula

25 / 54

Algorithm

The most commonly-used algorithm for the $L D L^{T}$ decomposition is the Bunch-Kaufman algorithm [5]
We omit the details here since it is pretty involved
Interested readers are referred to [4] and [5]
The computational complexity is $O (n^{3})$ , with a multiplicative factor similar to Cholesky decomposition

26 / 54

Implementation

Unfortunately, at the current moment there is no mature R interface to this decomposition
There is indeed a BunchKaufman() function in the Matrix package, but it is somewhat incomplete
The good news is that the algorithm has been implemented in the LAPACK library, which is included by R
We just need to write a simple C++ wrapper to call the function via Rcpp

27 / 54

Implementation

Simple wrapper for the factorization function

ldlt_fac = function(A)
{
    res = Matrix::BunchKaufman(A, uplo = "L")
    list(perm = res@perm, fac = matrix(res@x, res@Dim[1]))
}

28 / 54

Implementation

C++ code to call the solving function
This will create an R function ldlt_solve()

compiler_flags = "-lRlapack -lRblas -lgfortran -lm -lquadmath"
Sys.setenv("PKG_LIBS" = compiler_flags)
Rcpp::cppFunction(includes = "#include <R_ext/Lapack.h>",
code = "
    NumericVector ldlt_solve(List fac, NumericVector b)
    {
        NumericMatrix fac_res = fac[\"fac\"];
        IntegerVector perm = fac[\"perm\"];
        NumericVector sol = Rcpp::clone(b);
        const int n = fac_res.nrow();
        const int nrhs = 1;
        char uplo = 'L';
        int info;
        F77_CALL(dsytrs)(
            &uplo, &n, &nrhs, fac_res.begin(), &n,
            perm.begin(), sol.begin(), &n, &info FCONE);
        return sol;
    }
")

29 / 54

Implementation

Verify the result

set.seed(123)
n = 2000
M = matrix(rnorm(n^2), n)
A = M + t(M)
b = rnorm(n)
fac = ldlt_fac(A)
x = ldlt_solve(fac, b)
max(abs(A %*% x - b))  # Verify A*x = b

## [1] 8.482548e-12

30 / 54

Benchmark

This implementation is much faster than solve()

library(dplyr)
bench::mark(
    solve(A, b), ldlt_fac(A), ldlt_solve(fac, b),
    max_iterations = 10, check = FALSE
) %>% select(expression, min, median)

## # A tibble: 3 × 3
##   expression              min   median
##   <bch:expr>         <bch:tm> <bch:tm>
## 1 solve(A, b)           1.44s    1.44s
## 2 ldlt_fac(A)        813.09ms 813.09ms
## 3 ldlt_solve(fac, b)   3.44ms   4.09ms

31 / 54

When to Use?

As long as you can guarantee $A$ is symmetric, use $L D L^{T}$ decomposition to solve linear systems
If positive definiteness is guaranteed, use Cholesky decomposition

32 / 54

QR Decomposition33 / 54

Motivation

Most of the decomposition methods introduced before heavily rely on triangular matrices
This is because triangular matrices have cheap "inverse" operations
Another special type of matrices is the orthogonal matrix
$Q^{'} Q = Q Q^{'} = I$ , which implies $Q^{- 1} = Q^{'}$

34 / 54

QR Decomposition

QR decomposition factorizes a square matrix into the product of two matrices, $A = Q R$
$Q$ is an orthogonal matrix, $Q^{'} Q = Q Q^{'} = I$
$R$ is upper triangular

35 / 54

Factorization Theorem ^[2]

Let $A$ be a nonsingular square matrix. There exists a unique pair $(Q, R)$ , where $Q$ is an orthogonal matrix and $R$ is an upper triangular matrix with positive diagonal entries, such that $A = Q R$ .

36 / 54

Solving Linear Systems

Suppose the decomposition $A = Q R$ is given
If we wish to solve $A x = b$ , then:
First, compute $\tilde{b} = Q^{'} b$
Second, solve $R x = \tilde{b}$ to get $x$

37 / 54

Solving Linear Systems

Suppose the decomposition $A = Q R$ is given
If we wish to solve $A x = b$ , then:
First, compute $\tilde{b} = Q^{'} b$
Second, solve $R x = \tilde{b}$ to get $x$
However, it is uncommon to directly use QR decomposition for solving linear systems

37 / 54

Solving Linear Systems

Suppose the decomposition $A = Q R$ is given
If we wish to solve $A x = b$ , then:
First, compute $\tilde{b} = Q^{'} b$
Second, solve $R x = \tilde{b}$ to get $x$
However, it is uncommon to directly use QR decomposition for solving linear systems
Typically slower than LU decomposition
More useful in factorizing rectangular matrices

37 / 54

Factorization Theorem ^[3]

Let $A_{m \times n}$ be a matrix with $r a n k (A) = n$ , $n \leq m$ . Then there exist an orthogonal matrix $Q_{m \times m}$ and an upper triangular matrix $R_{n \times n}$ with positive diagonal entries, such that $A = Q (\begin{matrix} R \\ 0 \end{matrix}) = (\begin{matrix} Q_{1} & Q_{2} \end{matrix}) (\begin{matrix} R \\ 0 \end{matrix}) .$ In addition, the matrices $R$ and $Q_{1} = A R^{- 1}$ are uniquely determined.

38 / 54

Thin QR Decomposition

According to the factorization theorem in the previous slide, any rectangular matrix $A$ with full column rank can be factorized as $A = Q_{1} R$
$A \in R^{m \times n}$ , $Q_{1} \in R^{m \times n}$ , $R \in R^{n \times n}$
$Q_{1}$ is column-orthonormal, meaning that $Q_{1}^{'} Q_{1} = I_{n \times n}$
This is called the thin QR decomposition

39 / 54

Relation with Cholesky Decomposition

If the (thin) QR decomposition result $X = Q R$ is given
Then $X^{'} X = R^{'} Q^{'} Q R = R^{'} R$ , which is exactly the Cholesky decomposition of $A = X^{'} X$

40 / 54

Relation with Regression

To see why the thin QR decomposition is useful, recall the regression coefficient estimate $\hat{β} = (X^{'} X)^{- 1} X^{'} Y$ and predicted values $\hat{y} = X \hat{β}$
Suppose we have $X_{n \times p} = Q R$ , $X$ full column rank, then:
- $\hat{β} = (R^{'} R)^{- 1} R^{'} Q^{'} Y = R^{- 1} Q^{'} Y$
- $\hat{y} = Q R \hat{β} = Q Q^{'} Y$
$Q Q^{'}$ is essentially the projection matrix, or hat matrix, in regression analysis

41 / 54

Relation with Regression

To see why the thin QR decomposition is useful, recall the regression coefficient estimate $\hat{β} = (X^{'} X)^{- 1} X^{'} Y$ and predicted values $\hat{y} = X \hat{β}$
Suppose we have $X_{n \times p} = Q R$ , $X$ full column rank, then:
- $\hat{β} = (R^{'} R)^{- 1} R^{'} Q^{'} Y = R^{- 1} Q^{'} Y$
- $\hat{y} = Q R \hat{β} = Q Q^{'} Y$
$Q Q^{'}$ is essentially the projection matrix, or hat matrix, in regression analysis
Warning: $Q_{n \times p}$ is only column-orthonomal, so $Q Q^{'} \neq I_{n \times n}$ ! (We do have $Q^{'} Q = I_{p \times p}$ )

41 / 54

Algorithm

Here we omit the computing algorithm for QR decomposition
Interested readers are referred to
- Section 9 of [1] (modified Gram-Schmidt algorithm)
- Section 7.3.4 of [2] (Householder algorithm)
- Section 2.3.2 of [3] (Householder algorithm)
The important point is, in practice we do NOT explicitly form the $Q$ matrix
Instead, given a vector $y$ , computing $Q y$ and $Q^{'} y$ has specialized algorithms

42 / 54

Computational Complexity

For rectangular matrix $X_{n \times p}$ , $X$ full column rank, $n \geq p$
Computing the thin QR decomposition using the modified Gram-Schmidt algorithm costs $O (n p^{2})$
Using the Householder algorithm costs $O (n p^{2} - p^{3} / 3)$

43 / 54

Implementation

The qr() function in R can perform QR decomposition

set.seed(123)
x = matrix(rnorm(25), 5, 5)
qr_res = qr(x)

44 / 54

Implementation

The result is a compact representation of $Q$ and $R$

qr_res

## $qr
##             [,1]       [,2]       [,3]       [,4]       [,5]
## [1,]  1.67880106 -1.8735119 -0.1240544 -2.4977185 -0.6449736
## [2,]  0.13710826 -1.3836930 -1.2267898 -0.6009298  0.7682812
## [3,] -0.92846517  0.8909949 -0.7676374 -1.1355032  0.8695156
## [4,] -0.04199925 -0.4147299  0.9330131  0.3672150 -1.0253122
## [5,] -0.07701195 -0.1723435 -0.3178735 -0.8619799 -0.5906208
## 
## $rank
## [1] 5
## 
## $qraux
## [1] 1.3338547 1.0665197 1.1686505 1.5069425 0.5906208
## 
## $pivot
## [1] 1 2 3 4 5
## 
## attr(,"class")
## [1] "qr"

45 / 54

Implementation

To get the explicit $Q$ and $R$ matrices, use qr.Q() and qr.R()

qr.Q(qr_res)

##             [,1]       [,2]       [,3]        [,4]        [,5]
## [1,] -0.33385471 -0.7874465 -0.2822091  0.43404722 -0.02073790
## [2,] -0.13710826 -0.1474621 -0.2109068 -0.47031583  0.83293313
## [3,]  0.92846517 -0.3428718 -0.1241733  0.01466849  0.06897252
## [4,]  0.04199925  0.4395243 -0.8533937  0.27599706  0.02448081
## [5,]  0.07701195  0.2178078  0.3635610  0.71694943  0.54812026

qr.R(qr_res)

##          [,1]      [,2]       [,3]       [,4]       [,5]
## [1,] 1.678801 -1.873512 -0.1240544 -2.4977185 -0.6449736
## [2,] 0.000000 -1.383693 -1.2267898 -0.6009298  0.7682812
## [3,] 0.000000  0.000000 -0.7676374 -1.1355032  0.8695156
## [4,] 0.000000  0.000000  0.0000000  0.3672150 -1.0253122
## [5,] 0.000000  0.000000  0.0000000  0.0000000 -0.5906208

46 / 54

Implementation

But you rarely need to explicitly form $Q$
To compute $Q v$ and $Q^{'} v$ , use qr.qy() and qr.qty()

Q = qr.Q(qr_res)
v = rnorm(5)
Q %*% v

##             [,1]
## [1,] -0.65989192
## [2,]  1.65499813
## [3,] -1.80255035
## [4,] -0.11692776
## [5,] -0.02040374

qr.qy(qr_res, v)

## [1] -0.65989192  1.65499813 -1.80255035 -0.11692776 -0.02040374

47 / 54

Implementation

crossprod(Q, v)  # == t(Q) %*% v

##            [,1]
## [1,]  0.6394024
## [2,]  0.9249034
## [3,]  1.7073775
## [4,] -0.5390799
## [5,]  1.4027564

qr.qty(qr_res, v)

## [1]  0.6394024  0.9249034  1.7073775 -0.5390799  1.4027564

48 / 54

Implementation

The qr() function also supports thin QR decomposition

set.seed(123)
x = matrix(rnorm(15), 5, 3)
qr_res = qr(x)
qr.Q(qr_res)

##             [,1]       [,2]       [,3]
## [1,] -0.33385471 -0.7874465 -0.2822091
## [2,] -0.13710826 -0.1474621 -0.2109068
## [3,]  0.92846517 -0.3428718 -0.1241733
## [4,]  0.04199925  0.4395243 -0.8533937
## [5,]  0.07701195  0.2178078  0.3635610

qr.R(qr_res)

##          [,1]      [,2]       [,3]
## [1,] 1.678801 -1.873512 -0.1240544
## [2,] 0.000000 -1.383693 -1.2267898
## [3,] 0.000000  0.000000 -0.7676374

49 / 54

Implementation

You can also get the full QR decomposition by adding the complete = TRUE argument

qr.Q(qr_res, complete = TRUE)

##             [,1]       [,2]       [,3]        [,4]       [,5]
## [1,] -0.33385471 -0.7874465 -0.2822091 -0.23791265 0.36362704
## [2,] -0.13710826 -0.1474621 -0.2109068  0.95639468 0.01684644
## [3,]  0.92846517 -0.3428718 -0.1241733  0.05201684 0.04760905
## [4,]  0.04199925  0.4395243 -0.8533937 -0.11881268 0.25031427
## [5,]  0.07701195  0.2178078  0.3635610  0.10901648 0.89586144

qr.R(qr_res, complete = TRUE)

##          [,1]      [,2]       [,3]
## [1,] 1.678801 -1.873512 -0.1240544
## [2,] 0.000000 -1.383693 -1.2267898
## [3,] 0.000000  0.000000 -0.7676374
## [4,] 0.000000  0.000000  0.0000000
## [5,] 0.000000  0.000000  0.0000000

50 / 54

Benchmark

library(Matrix)
set.seed(123)
M = matrix(rnorm(2000^2), 2000)
A = crossprod(M)
bench::mark(
    lu(A), chol(A), qr(A),
    max_iterations = 10, check = FALSE
) %>% select(expression, min, median)

## # A tibble: 3 × 3
##   expression      min   median
##   <bch:expr> <bch:tm> <bch:tm>
## 1 lu(A)         1.32s    1.32s
## 2 chol(A)       1.27s    1.27s
## 3 qr(A)         4.18s    4.18s

51 / 54

Benchmark

set.seed(123)
n = 2000
p = 200
x = matrix(rnorm(n * p), n, p)
bench::mark(
    chol(crossprod(x)),
    qr(x),
    max_iterations = 100, check = FALSE
) %>% select(expression, min, median)

## # A tibble: 2 × 3
##   expression              min   median
##   <bch:expr>         <bch:tm> <bch:tm>
## 1 chol(crossprod(x))   42.2ms   45.1ms
## 2 qr(x)                57.6ms   58.2ms

52 / 54

When to Use?

QR decomposition is seldom used to solve linear systems directly
- It is typically slower than LU decomposition
Thin QR decomposition is widely used in regression computation
- It is slightly slower than Cholesky decomposition on $X^{'} X$
- But QR decomposition is more stable

53 / 54

References

[1] Folkmar Bornemann (2018). Numerical Linear Algebra. Springer.

[2] Grégoire Allaire and Sidi Mahmoud Kaber (2008). Numerical linear algebra. Springer.

[3] Åke Björck (2015). Numerical methods in matrix computations. Springer.

[4] James R. Bunch and Beresford N. Parlett (1971). Direct methods for solving symmetric indefinite systems of linear equations. SIAM Journal on Numerical Analysis.

[5] James R. Bunch and Linda Kaufman (1977). Some stable methods for calculating inertia and solving symmetric linear systems. Mathematics of computation.

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

Computational Statistics

Lecture 3

Yixuan Qiu

2023-09-20

Numerical Linear Algebra

Today's Topics

Spline Fitting

Interpolation Problem

Spline Fitting

Natural Cubic Spline

Natural Cubic Spline

Theorem

Spline Fitting

Spline Fitting

Back to Regression

First improvement

Principle 1

Second improvement

Principle 2

Third improvement

Principle 3

Principle 4

LDLTLDLT Decomposition

Motivation

LDLTLDLT Decomposition

Solving Linear Systems

Solving Linear Systems

Algorithm

Implementation

Implementation

Implementation

Implementation

Benchmark

When to Use?

QR Decomposition

Motivation

QR Decomposition

Factorization Theorem [2]

Solving Linear Systems

Solving Linear Systems

Solving Linear Systems

Factorization Theorem [3]

Thin QR Decomposition

Relation with Cholesky Decomposition

Relation with Regression

Relation with Regression

Algorithm

Computational Complexity

Implementation

Implementation

Implementation

Implementation

Implementation

Implementation

Implementation

Benchmark

Benchmark

When to Use?

References

Numerical Linear Algebra

Help

$L D L^{T}$ Decomposition

$L D L^{T}$ Decomposition

Factorization Theorem ^[2]

Factorization Theorem ^[3]