Computational Statistics
Lecture 10
Yixuan Qiu
2023-11-22
Simulation and Sampling
Today's Topics
Some classical problems
Inverse transform algorithm
Rejection sampling
Problem
Given a probability distribution ν, generate random variables X1,…,Xn from ν
ν can be specified in different forms
Distribution function F(x)
Density/Mass function p(x)
Unnormalized density/mass function q(x)∝p(x)
Some general description of the distribution
Why We Need Sampling
Many quantities of interest in statistics can be written as expectations of random variables, expressed as high-dimensional integrals:
I=EX[f(X)]=∫f(x)p(x)dx,X∼p(x).
In many cases we are unable to evaluate I exactly, but it is possible to find an unbiased estimator for I:
ˆI=1MM∑i=1f(Xi),Xi∼p(x), i=1,…,M.
The key challenge is to generate X1,…,XM∼p(x).
Example - EM Algorithm
To maximize the marginal likelihood L(θ;X)=∫p(X|Z,θ)p(Z|θ)dZ, EM algorithm consists of two steps:
Expectation: Define Q(θ|θ(t))=EZ|X,θ(t)[logL(θ;X,Z)]
Maximization: Solve θ(t+1)=argmaxθ Q(θ|θ(t))
Example - EM Algorithm
When Q(θ|θ(t)) has no closed form, it needs to be approximated by Monte Carlo samples from p(Z|X,θ(t)).
This method is typically called Monte Carlo expectation-maximization (MCEM).
Example - Bayesian Statistics
At the core of Bayesian statistics is the sampling from posterior distribution p(θ|x)∝p(θ,x)=π(θ)p(x|θ).
In this case, p(θ|x) is given in the unnormalized form, since we only have access to p(θ,x)=π(θ)p(x|θ).
Pseudo Random Number
Strictly speaking, it is unlikely to get "real" random numbers in computers
What existing algorithms generate are pseudo random numbers
We omit these technical details
Instead, we assume there is a "generator" that can produce independent random variables U1,U2,… that follow the uniform distribution Unif(0,1)
Our target is to generate other random numbers based on U1,U2,…
Classical Problems
Classical Problems
Random permutation
One-pass random selection
Generating normal random variables
Random Permutation
Problem: Generate a permutation of 1,…,n such that all n! possible orderings are equally likely.
Random Permutation
Problem: Generate a permutation of 1,…,n such that all n! possible orderings are equally likely.
Widely used in sampling without replacement
Can select only a subset
Algorithm
A simple and natural method:
Generate a sequence of uniform random numbers U1,…,Un
Sort U1,…,Un and record their orders I1,…,In
That is, UI1≤⋯≤UIn
Then I1,…,In is a random permutation of 1,…,n
The complexity of this algorithm is O(nlog(n))
Algorithm
A better algorithm is as follows [1]:

Here Int(x) is the largest integer less than or equal to x
This is known as the Fisher-Yates shuffling algorithm
Complexity is O(n)
Proof Sketch
For each k, I follows a (discrete) uniform distribution on [k]:={1,2,…,k}
When k=n, P(Pn=i)=1/n for i∈[n]
When k=n−1, P(Pn−1=i|Pn=pn)=1/(n−1) for i∈[n]∖{pn}
When k=n−2, P(Pn−2=i|Pn=pn,Pn−1=pn−1)=1/(n−2) for i∈[n]∖{pn,pn−1}
By reduction, we have P(P1=p1,…,Pn=pn)=1/n!, where {p1,…,pn} is a permutation of [n]
One-Pass Random Selection
Problem: Suppose that there is a sequence of nonnegative numbers a1,…,an, and one can access them sequentially. The task is to randomly select an index i∗ such that P(i∗=i)=ai/∑nj=1aj, with only one pass of data access.
One-Pass Random Selection
Problem: Suppose that there is a sequence of nonnegative numbers a1,…,an, and one can access them sequentially. The task is to randomly select an index i∗ such that P(i∗=i)=ai/∑nj=1aj, with only one pass of data access.
Useful when accessing data is expensive
For example, reading data from hard disks
Can be extended to multiple independent selections
Algorithm [2]

We need to show that P(i∗=i)=ai/Sn for i=1,…,n, where Sk=∑kj=1aj.
Proof Sketch
Now we attempt to prove a stronger conclusion: after \require{color}\color{deeppink}{k} iterations, we have P(i^*=i)=a_i/S_k for i=1,\ldots,k
Clearly this holds for k=1
Suppose that the result holds for k=l, and then in the (l+1)-th iteration:
- For i=1,\ldots,l, i^*=i means that in the new iteration i^* is not updated
- For i=l+1, i^*=l+1 means i^* is updated
- The probability of updating is a_{l+1}/S_{l+1}, which is exactly P(i^*=l+1)
- Finally, for i=1,\ldots,l, P(i^*=i)=(a_i/S_l)\cdot(1-a_{l+1}/S_{l+1})=a_i/S_{l+1}
Generating Normal Random Variables
Problem: Given a uniform random number generator, simulate random variables X_1,\ldots,X_n\overset{iid}{\sim}N(0,1).
Generating Normal Random Variables
Problem: Given a uniform random number generator, simulate random variables X_1,\ldots,X_n\overset{iid}{\sim}N(0,1).
Foundation of many simulation algorithms
Extensively studied
Many different algorithms
Box-Muller Transform
Generate two independent uniform random numbers U_1 and U_2
Let Z_1=\sqrt{-2\log(U_1)}\cos(2\pi U_2) and Z_2=\sqrt{-2\log(U_1)}\sin(2\pi U_2)
Then Z_1 and Z_2 are two independent N(0,1) random variables
Box-Muller Transform
Generate two independent uniform random numbers U_1 and U_2
Let Z_1=\sqrt{-2\log(U_1)}\cos(2\pi U_2) and Z_2=\sqrt{-2\log(U_1)}\sin(2\pi U_2)
Then Z_1 and Z_2 are two independent N(0,1) random variables
Requires evaluating functions \log(x), \sqrt{x}, \sin(x), and \cos(x)
May be inefficient when lots of random numbers are required
Inverse Transform Algorithm
Using the general inverse transform algorithm (introduced later):
Generate uniform random number U
Set Z=\Phi^{-1}(U), where \Phi(x) is the c.d.f. of N(0,1)
Inverse Transform Algorithm
Using the general inverse transform algorithm (introduced later):
Generate uniform random number U
Set Z=\Phi^{-1}(U), where \Phi(x) is the c.d.f. of N(0,1)
- However, computing \Phi^{-1}(\cdot) may be difficult and inefficient
Ziggurat Method
Essentially a carefully designed rejection method (introduced later). From [3]:
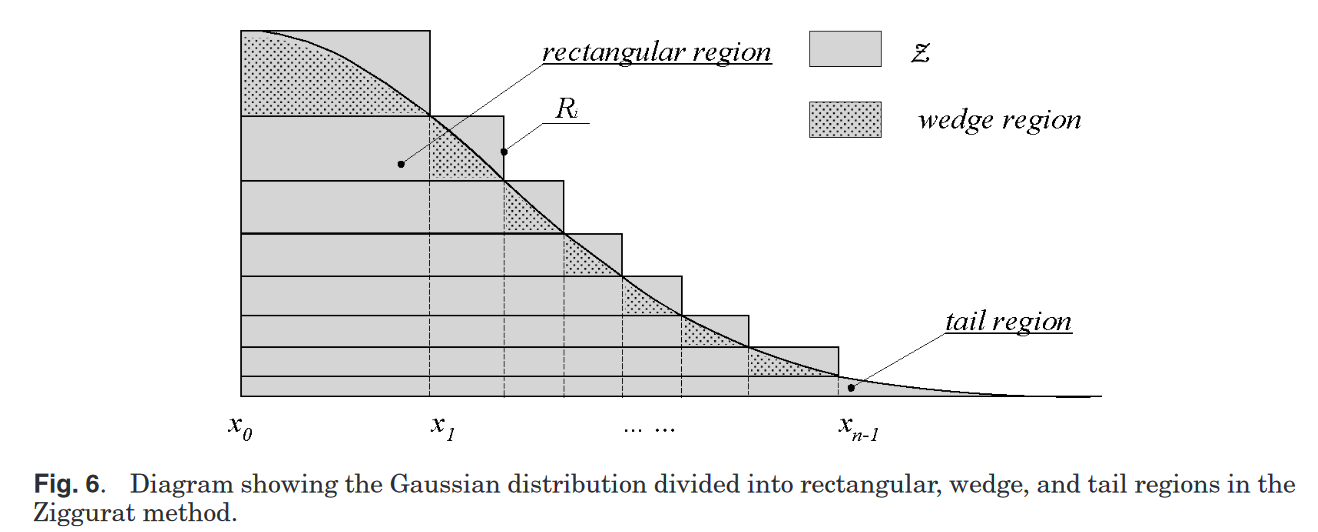
Ziggurat Method
Essentially a carefully designed rejection method (introduced later). From [3]:

- Practically one of the most efficient methods to generate normal random numbers
Implementation
We do a simple comparison between R's built-in rnorm() and various normal random number generators based on the Ziggurat method.
library(dplyr)library(bench)library(dqrng)library(RcppZiggurat)bench::mark( rnorm(1e7), dqrnorm(1e7), zrnorm(1e7), min_iterations = 10, max_iterations = 10, check = FALSE) %>% select(expression, min, median)## # A tibble: 3 × 3## expression min median## <bch:expr> <bch:tm> <bch:tm>## 1 rnorm(1e+07) 417.7ms 420.4ms## 2 dqrnorm(1e+07) 94.9ms 99.9ms## 3 zrnorm(1e+07) 73.1ms 75.6msUnivariate random number generation
Inverse transform algorithm
Rejection sampling
Inverse Transform Algorithm
Discrete Distribution
Suppose we have a discrete distribution with the following probability mass function:
p(x_i)\equiv P(X=x_i)=p_i,\quad i=0,1,\ldots,\ \sum_j p_j=1
The following algorithm [1] can be used to generate X\sim p(x):
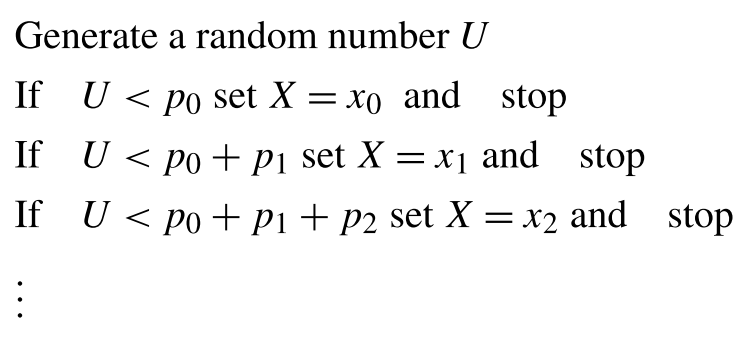
Discrete Distribution
This procedure can be compactly expressed as X=F^{-1}(U), where F(\cdot) is the c.d.f. of X, and F^{-1}(\cdot) is the (generalized) inverse c.d.f.:
F^{-1}(p)=\inf\,\{x\in\mathbb{R}:p\le F(x)\}.
This is why this method is called the inverse transform algorithm for discrete distributions.
Continuous Distribution
For continuous distributions, the algorithm is more straightforward. To generate X\sim p(x):
Generate uniform random number U
Set X=F^{-1}(U), where F(x) is the c.d.f. of X
Proof Sketch
To prove that X\sim p(x), we only need to show P(X\le x)=F(x):
\begin{align*} P(X\le x) & =P(F^{-1}(U)\le x) & & \text{(by algorithm)}\\ & =P(U\le F(x)) & & \text{(monotonicity of }F(\cdot)\text{)}\\ & =F(x) & & \text{(c.d.f of uniform distribution)} \end{align*}
Challenge
In general, the inverse transform algorithm only applies to univariate distributions (but we have a generalized method called measure transport)
Also, evaluating F^{-1}(\cdot) may be difficult
Example
Consider the exponential distribution with mean 1, whose distribution function is given by F(x)=1-e^{-x}
Using the inverse transform algorithm we have X=-\log(1-U)
Since 1-U also follows \mathrm{Unif}(0,1), we can simply do X=-\log(U)
To generate exponential random variable with mean \theta, we have X=-\theta\log(U)
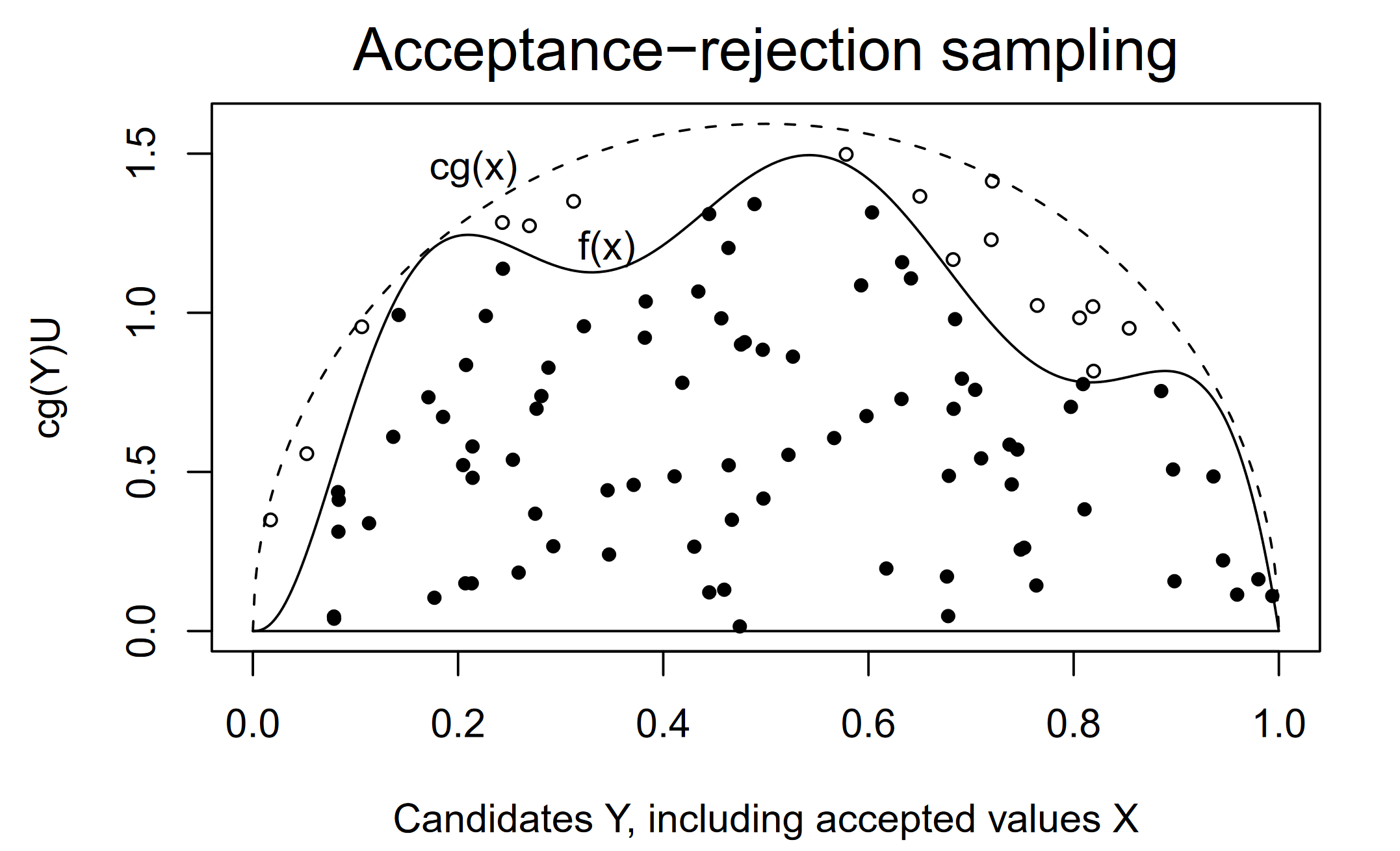
Rejection Sampling
Rejection Sampling
Rejection sampling is a general technique for exact sampling. It applies to both discrete and continuous distributions, and is not limited to univariate distributions.
Suppose we want to generate X\sim f(x), and we have an existing method to sample from another distribution X\sim g(x). f(x) and g(x) can be interpreted as probability mass functions or density functions.
Rejection Sampling
Let c>0 be a constant such that f(x)/g(x)\le c for all x\in\mathcal{X}, where \mathcal{X} stands for the support of g(x).
Then the rejection sampling method proceeds as follows:
Generate Y\sim g(y)
Generate a uniform random number U
If U\le f(Y)/[cg(Y)], set X=Y. Otherwise return to Step 1.
Diagram
From [1]:

(For discrete distribution)
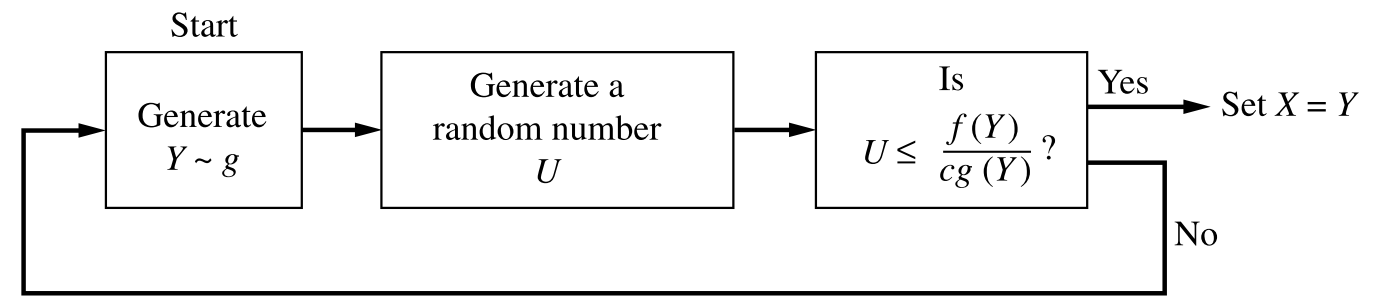
(For continuous distribution)
Theorem [1]
The generated random variable X follows f(x).
The number of iterations of the algorithm is a geometric random variable with mean c.
Theorem [1]
The generated random variable X follows f(x).
The number of iterations of the algorithm is a geometric random variable with mean c.
Question: What is the best possible value of \require{color}\color{deeppink}{c} ?
Proof Sketch
P(\text{accepted}|Y=y)=f(y)/[cg(y)]
P(\text{accepted})=\int P(\text{accepted}|Y=y)g(y)\mathrm{d}y=1/c
Let \mathcal{X}=(-\infty,x_1]\times\cdots\times(-\infty,x_p], and then
\small\begin{align*} P(X\in\mathcal{X}) & =P(Y\in\mathcal{X},\text{accepted})+(1-1/c)P(X\in\mathcal{X})\\ & =\int_{\mathcal{X}}P(\text{accepted}|Y=y)g(y)\mathrm{d}y+(1-1/c)P(X\in\mathcal{X})\\ & =(1/c)\int_{\mathcal{X}} f(y)\mathrm{d}y+(1-1/c)P(X\in\mathcal{X}) \end{align*}
- This shows that P(X\in\mathcal{X})=\int_{\mathcal{X}} f(y)\mathrm{d}y
Geometric Interpretation
Consider the set
\mathcal{S}_{M}(h)=\{(x,z):0\le z\le Mh(x),x\in\mathbb{R}^{p},z\in\mathbb{R}\},
where h is a density function, and M>0 is a constant.
We show that if (X,Z)\sim \mathrm{Unif}(\mathcal{S}_{M}(f)), then X\sim f(x).
Geometric Interpretation
Let \mathcal{S}=\mathcal{S}_{M}(f) and \mathcal{X}=(-\infty,x_1]\times\cdots\times(-\infty,x_p], and then by definition,
\begin{align*} P(X\in\mathcal{X}) & =\frac{\mathrm{vol}(\mathcal{S}\cap\mathcal{X}\times[0,+\infty))}{\mathrm{vol}(\mathcal{S})}=\frac{\int_{\mathcal{X}}\int_{0}^{Mf(x)}\mathrm{d}z\mathrm{d}x}{\int_{\mathbb{R}^{p}}\int_{0}^{Mf(x)}\mathrm{d}z\mathrm{d}x}\\ & =\int_{\mathcal{X}}f(x)\mathrm{d}x, \end{align*}
which proves that X has density f(x).
Conversely, if X\sim h(x) and Z|\{X=x\}\sim \mathrm{Unif}(0,Mh(x)), then (X,Z)\sim \mathrm{Unif}(\mathcal{S}_{M}(h)).
Challenge
Finding a good proposal distribution g(x) can be hard
Finding the constant c is even harder
Rejection sampling may "waste" a lot of random numbers
If f(x) is high-dimensional, the problem would be much more challenging
References
[1] Sheldon M. Ross (2011). Simulation. Academic Press.
[2] Michael W. Mahoney (2016). Lecture notes on randomized linear algebra. arXiv:1608.04481.
[3] David B. Thomas et al. (2007). Gaussian random number generators. ACM Computing Surveys.